纳米复合材料压阻式薄膜超声传感器近场干扰抑制方法

时间：

　　论文《纳米复合材料压阻式薄膜超声传感器近场干扰抑制方法》发表在《仪器仪表学报》，版权归《仪器仪表学报》所有。本文来自网络平台，仅供参考。

　　摘要

　　与常规超声传感器相比，基于纳米石墨烯/聚乙烯吡咯烷酮(GNP/PVP)的柔性压阻式薄膜超声传感器具有轻质、柔性、宽频带、易集成，且能够与曲面表面共形贴合的优点，在无损检测与结构健康监测领域展现出了良好的应用前景。然而，当压阻式薄膜超声传感器与超声发射装置距离较近、传感器与转换电路的连接方式不稳定或测试系统电磁屏蔽设计失效时，会引入较大的电磁干扰，导致强烈的信号串扰，影响近场范围内的声场信息获取及超声信号质量。为了有效抑制串扰信号，分别采用移相与差分放大补偿方法以及基于互相关的迭代逼近方法实现超声信号的重构。实验结果表明，移相与差分放大补偿方法处理后的信号可以有效去除利用GNP/PVP压阻式薄膜超声传感器接收到超声信号的串扰;基于互相关的迭代逼近方法能够使得串扰信号的区间方差减少99.18%，从而更有效地抑制了串扰对超声信号的干扰。

原理图

　　关键词

　　纳米GNP/PVP压阻式薄膜超声传感器;近场干扰;串扰抑制

　　0 引言

　　超声无损检测是一种在现代工业中至关重要的检测方法，广泛应用于航空航天、汽车制造和能源等多个领域，用于检测材料中的缺陷以及评估结构完整性等[1-4]。超声传感器是其中的核心组件，通过发射和接收超声波，分析波形的反射、散射和衰减等特征，实现对材料内部情况的检测[5-8]。

　　近年来，柔性超声传感器在超声无损检测中的应用日益增加[5,9-12]。在理论研究方面，研究人员还提出了基于有效介质理论分析模型，讨论了填料形状、隧道效应和不同接触方式等因素，以解释此类压阻传感器的传感机理[13-15]。在此基础上，研究人员们利用了炭黑[16]、碳纳米管[17]、石墨烯[13]、金属纳米颗粒[18]和金属纳米线[19]等导电填充物，通过旋涂[20]、刮涂[21]、3D打印等工艺[22]成功制备出了多种具有良好灵敏度和稳定性的复合材料薄膜传感器，并且在超声无损检测领域逐步展开了应用。

　　压阻式薄膜超声传感器作为超声无损检测的前沿和热点，正逐步改变传统硬质传感器在实际应用中的局限性[6]。柔性压阻式薄膜超声传感器因其重量轻、成本低、柔韧性高和制作相对容易等优点[23-24]，能够贴附在各种复杂表面，或是嵌入复合材料结构内部，能够检测由结构内部损伤引起的超声波的变化，从而在结构健康监测等领域展现出巨大潜力[25-26]。然而，压阻式薄膜超声传感器的应用往往依赖于转换电路，通过将超声传播引起的电阻变化转化为与之成线性关系的电压变化。目前仅依靠压阻式薄膜超声传感器难以产生有效的超声振动激励，在实际应用过程中仅作为接收器，仍需其他激励源(如压电陶瓷片或激光器)结合功率放大器产生振动，并且其固有噪声水平较高[27]。

　　功率放大器产生的高频高压激励信号通常会以电磁干扰的形式进一步限制压阻薄膜传感器在被测结构上的应用。与传导干扰[28]或相控阵阵元间的超声波串扰不同[29]，这类干扰信号会通过电磁波形式从传感元件接口电路引入干扰，其幅值大小与传感元件到干扰源的距离正相关[30]。在振动源的近场区域内，该干扰通常不容忽视，会覆盖接收信号中发射信号对应的时间区域，导致该区域信号畸变甚至被淹没，失去近场范围内的声场信息。同时，串扰的存在还会限制信号的放大倍数。当提高放大模块的增益使放大器输出信号进入饱和区时，由于串扰信号的幅值较大，这会进一步降低反馈回路的稳定性，增加系统的非线性失真，进而引发后续时间段内传感信号的振荡。此类振荡现象会严重降低超声信号的信噪比，并对传感过程的稳定性产生负面影响。

　　为了抑制外部引入的串扰分量，拓展声场信息的获取范围，提升超声信号的质量和传感过程的稳定性，本文在所制备的GNP/PVP压阻式薄膜超声传感器的基础上，通过移相与差分放大补偿方法、基于互相关的迭代逼近方法，抑制传感信号中的串扰分量并分离被串扰分量覆盖的超声信号波形，进而提升压阻式薄膜传感器信号的稳定性。

　　1 近场干扰抑制方法

　　1.1 移相模块

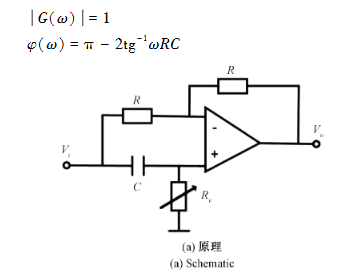
　　移相模块[31]原理如图1(a)所示，其全频带范围内的幅频特性|G(ω)|平坦，相频特性φ(ω)受电阻值R₁与电容值C影响。通过改变R₁的大小可以调整特定频率ω下输入信号Vᵢ的相位，并起到时间延迟的作用，其频率特性见相关公式。当选择C=1 nF，Rᵥ的变化范围为0~5 kΩ时，其相频特性如图1(b)所示，对于频率为200 kHz的信号将产生90°~180°的超前相移，从而使信号在时间上发生移动。

　　(图1 移相模块 Fig. 1 Phase shifting module：(a)原理 (a) Schematic;(b)相频特性 (b) Phase-frequency characteristics)

　　1.2 差分放大模块

　　使用仪表放大器AD8421结合外围电路构成的差分放大模块如图2所示。AD8421的内部拓扑结构由两级组成，前一级是提供差分放大的前置放大器，其后是一个抑制共模电压的差动放大器。该模块输入信号Vᵢ₊、Vᵢ₋与输出信号V₀之间的关系如相关公式所示，该模块可以抑制输入信号Vᵢ₊、Vᵢ₋中的共模信号，放大差模信号。本文参考信号S_R与传感信号S_S中串扰分量具有高度相似性，调节信号的相位偏移与增益倍数后输入差分放大模块，即可大幅度抑制传感信号中的串扰分量。

　　(图2 差分模块原理 Fig. 2 Differential module schematic diagram)

　　1.3 基于互相关的迭代逼近方法

　　不同于使用移相与差分放大模块组合的方式进行串扰抑制，基于互相关的迭代逼近方法从数据处理的角度出发实现串扰抑制。由于参考信号S_R与传感信号S_S中串扰分量在时间上存在延迟、在幅值上存在差异，故两信号做差后仍存在残余分量。通过迭代对参考信号S_R进行j(j=1,2,3,…)次平移(平移点数为ΔN)，抑制传感信号S_S与参考信号S_R中串扰分量在时间上的偏差，寻找对参考信号S_R进行倍乘的最佳放大倍数k，以尽可能使两信号中的串扰分量接近，从而通过做差去除传感信号中的串扰分量，其流程如图3所示。

　　(图3 基于互相关的迭代逼近方法流程 Fig. 3 Flowchart of iterative approximation method based on cross-correlation)

　　基于互相关的迭代逼近方法具体步骤如下：

　　1. 初始化参数：矩形窗初始宽度p₀=400000(与激发信号中汉宁窗的宽度相等)，初始比例系数k₀=V_Spp/V_Rpp(避免因两信号中串扰分量幅值差异过大导致无法收敛，其中V_Spp和V_Rpp分别代表信号S_S₁和S_R₁的峰峰值)，偏移点数ΔN₀=0，并通过公式对信号S_S和S_R去直流。

　　去直流公式：(x_{der}(n) = x(n) - frac{1}{N_t} sum_{n=0}^{N_t-1} x(n))，式中x_der(n)表示去直流分量后的信号，N_t为信号总点数。

　　2. 构造互相关函数R(τ)：(R_j( au) = sum_{n=-N_i}^{N_r} S_{S_j}(n) S_R(n+ au) W_{p_j}(n+ au))，其在距离激发时刻最近的极大值点的横坐标代表参考信号与传感信号中串扰分量在时间上的偏差，该偏差用平移点数ΔN表示。式中W_pj(n+τ)表示宽度为p的矩形窗信号，用于进一步提升互相关函数的准确度，即增加对未与超声信号重叠的串扰信号区间(N₀, N₀+p)的预测，抑制在求解互相关函数过程中非串扰分量对平移点数ΔN产生的偏差，N₀代表激发时刻对应的信号点数。

　　3. 信号调整与优化：求得偏差点数后对信号S_R进行左移操作，使两信号的串扰部分在水平方向尽可能重合;随后对信号S_R进行幅值放缩，求解其与信号S_S在区间(N₀, N₀+p)内差的方差最小值σₘ，以估计最佳比例系数k_opt。

　　4. 带通滤波与包络拟合：记(S_S(n) - S_R(n+ΔN)·k_opt)为经过平移与倍乘处理后的信号S_dj，对其进行带通滤波以剔除信号中的高频噪声(滤波器中心频率为200 kHz，带宽为10 kHz)。在区间(N₀, N₀+p₀)内求解信号S_dj的极大值点，由于本文使用汉宁窗调制的5周期正弦脉冲信号作为发射信号，根据兰姆波的传播特性[32]，最先到达并与串扰信号重叠的是S₀模态，因此选择使用汉宁窗曲线拟合S₀模态的包络曲线。选定初始汉宁窗时域曲线(W_N(n) = 0.5 - 0.5cos(frac{2pi n}{N}))，通过使传感信号S_S在可能与串扰分量重叠的区间内(N₀, N₀+p₀)的各极大值点到汉宁窗曲线的距离最短，拟合作为待估计参数的窗宽、幅值和起始点数，确定S₀模态的近似包络曲线，通过这种拟合估计超声信号的到达时间(N₀+p)，进而确定所估计的与超声信号不重叠的串扰信号区间(N₀, N₀+p)。

　　5. 迭代收敛判断：为了进一步提高对超声信号到达时间估计的准确性，对上述操作进行迭代处理。在迭代过程中，对信号S_R和S_R·W_pj(表示被施加变化矩形窗的串扰信号，逐步逼近未重叠部分的串扰分量)进行处理，通过计算收敛因子L来确定迭代的收敛过程和估计的准确程度。收敛因子L的表达式如下：(L_j = frac{sigma_{m_j} - sigma_{m_{j-1}}}{sigma_{m_j} - sigma_{m_0}})。当收敛因子的绝对值小于收敛阈值(本文设置为0.05)，认为所估计超声信号到达时间的准确程度已经可以接受，取方差σ_mj中最小值所对应迭代次数的输出结果为信号的最终处理结果。

　　2 实验设置

　　2.1 材料

　　本文所采用材料如下：石墨烯纳米颗粒(G196544，阿拉丁生化科技股份有限公司)、聚乙烯吡咯烷酮(P766521，麦克林生化科技股份有限公司)、无水乙醇(10009218，国药集团化学试剂有限公司)和聚酰亚胺膜等。所用的被测样品为玻璃纤维增强聚合物板(简称玻纤板)和铝板。

　　2.2 GNP/PVP压阻式薄膜超声传感器制备

　　压阻式薄膜超声传感器(简称薄膜)的制备采用喷涂的方式[13]：

　　1. 首先，将0.3 g石墨烯纳米颗粒与1.7 g PVP加入80 mL无水乙醇中，构成GNP/PVP的分散液。

　　2. 磁力搅拌1800 s后，使用超声清洗机清洗分散液21600 s，以分散石墨烯纳米颗粒。

　　3. 随后将经过超声分散的GNP/PVP分散液装填入空气喷枪，通过空气压缩将其雾化为细小液滴。

　　4. 最终，在空气气流的引导下稳定均匀地沉积在聚酰亚胺膜表面，形成薄膜。

　　5. 将制备完成的薄膜剪裁成1 cm×1 cm的正方形，用于测试。

　　2.3 玻纤板测试实验设置

　　在玻纤板的一侧布置制备好的薄膜，其中薄膜S被紧密贴合在玻纤板表面上，用以接收超声信号;薄膜R放置于薄膜S邻近处并悬浮，使其能够接收到不通过板而直接在空间中传播的串扰信号，如图4(a)、(c)所示。在各薄膜表面制备银电极，随后在银电极上粘贴导电铜胶带并连接至屏蔽线缆，接入至转换电路的输入端。在距离薄膜2、6、8、14 cm处分别粘贴直径为10 mm、厚度为0.5 mm的压电陶瓷圆片Aᵢ(i=1,2,3,4)，作为超声信号激励源。由信号发生器通过功率放大器对压电陶瓷片施加中心频率为200 kHz的汉宁窗调制5周期正弦脉冲信号，产生有效的振动。测试系统的连接方式如图4(b)所示，薄膜经过初级信号转换模块实现电阻-电压转换及固定增益放大;经过移相模块、滤波和放大模块后接入差分放大模块，电路的输出端连接至示波器以读取数据并观察超声波形。

　　(图4 基于GNP/PVP压阻式薄膜超声传感器的玻纤板超声测试 Fig. 4 Ultrasonic testing of fiberglass plate based on GNP/PVP piezoresistive film ultrasonic sensor：(a)测试布置示意图;(b)系统连接图;(c)实物布置图)

　　2.4 铝板测试实验设置

　　将压电陶瓷片和薄膜以同样方式粘贴在铝板上，间距为2 cm。连接所需的信号线和屏蔽层(地线)分别焊接在薄膜的两电极上，随后接入转换电路并连接至示波器。

　　3 玻纤板实验结果

　　在玻纤板上的测试结果如图5所示。薄膜R所产生的参考信号S_Ri仅包含由高频交变电压引起的电路串扰现象;压电陶瓷片Aᵢ振动引起薄膜S产生的传感信号S_Si同时包含串扰分量和超声信号。由于电路输入端接入的薄膜等效电路模型、位置分布存在细微差异，因此信号S_Si(i=1,2,3,4)与S_Ri中的串扰信号在时间上存在延迟、幅值上存在不同，利用参考信号S_Ri通过移相器与差分放大补偿和基于互相关迭代逼近的信号处理方法，对传感信号S_Si中的串扰分量进行消减。

　　(图5 压电陶瓷片Aᵢ振动引起薄膜S产生的传感信号S_Si与薄膜R所产生的参考信号S_Ri Fig. 5 The sensing signal S_Si generated by the film S due to the vibration of the PZT Aᵢ and the reference signal S_Ri generated by the film R)

　　3.1 移相与差分放大补偿方法

　　压电陶瓷片Aᵢ振动引起薄膜S产生的传感信号S_Ai与薄膜R所产生的参考信号S_Ri存在一定的相位偏差。对各信号通道接入移相模块，改变电阻值R_V对波形相位进行调节。信号S_Ri仅包含与S_Ai相似的串扰分量，而不包含由超声振动导致薄膜电阻变化而引起的超声信号，故可以通过差分模块大大抑制其中的共模分量(即串扰分量)。当薄膜与激励源距离较近时，超声信号将与串扰信号重叠(即A₁发射时)，调节电阻值R₁的大小补偿传感信号与串扰信号的偏差，同时调整两信号的硬件增益倍数，实现对两信号中串扰分量的增益补偿，从而大幅还原出被串扰分量所覆盖的超声信号，如图6所示。

　　(图6 移相与差分放大补偿方法处理结果 Fig. 6 Results of phase shifting and differential amplification compensation method：(a)信号S_S1与S_R1经过差分放大后的输出信号;(b)信号S_S1与经过差分放大后的输出信号对比)

　　3.2 基于互相关的迭代逼近方法

　　以压电陶瓷片A₁发射、薄膜S所接收到的信号为例进行讨论。根据基于互相关的迭代逼近方法，在给定收敛因子阈值的条件下，可通过少次迭代使结果快速收敛，并且给出最佳的平移常数ΔN和比例系数k_opt。

　　3.2.1 加窗对互相关函数的影响

　　在迭代过程中，针对不同矩形窗的宽度得到的互相关函数及其最小局部极大值所对应的点数如图7(a)和表1所示，对应加窗处理的串扰信号如图7(b)所示。可以观察到，不同窗宽对应的偏移点数存在较大差异，这是由于与串扰信号重叠的传感信号所导致的。当矩形窗所对应的区间(N₀, N₀+W)内无超声信号时(即仅包含串扰分量)，则可以求得最精确的偏移点数ΔN_c。

　　(图7 迭代处理的互相关函数和加窗串扰对比 Fig. 7 Comparison of cross-correlation function and windowed crosstalk in iterative processing：(a)迭代过程中的互相关函数;(b)迭代过程中的加窗串扰信号)

　　3.2.2 收敛因子的作用

　　收敛因子L表示迭代的收敛过程和估计的准确程度，当收敛因子的绝对值小于收敛阈值(本文设置为0.05)，即认为所估计超声信号到达时间的准确程度已经可以接受，并取方差σ_mj中最小值所对应迭代次数的输出结果为信号的最终处理结果。

　　3.2.3 实验结果

　　通过对比可以得到，经过基于互相关的迭代逼近方法处理后的信号S_dj的串扰部分经过3次迭代后有显著削弱，如图8(a)所示。经过3次迭代，收敛因子L和方差迅速衰减，其中收敛因子在第3次迭代时下降为0.03，落入收敛区间并结束迭代，如图8(b)所示;方差从初始的220.6846×10⁵迅速下降至1.8105×10⁵，衰减了99.18%。

　　表1 迭代过程中的参数变化 Table 1 Parameter variation during the iterative process

　　|-|--|-||-||

　　| 1 | 237723 | 1.0000 | 220.6846 | 0.9626 | 60899 |

　　| 2 | 148293 | 0.1032 | 10.7846 | 0.9380 | -2205 |

　　| 3 | 152943 | 0.0300 | 1.8105 | 0.9451 | -575 |

　　(图8 基于互相关的迭代逼近方法处理结果对比 Fig. 8 Comparison of results from iterative approximation method based on cross-correlation：(a)基于互相关的迭代逼近方法处理后的信号与汉宁窗拟合信号;(b)收敛因子与方差)

　　4 讨论

　　电磁干扰源、传播途径和敏感源作为干扰产生的3个基本要素，欲解决电磁兼容问题，可分别从接地设计、电磁屏蔽、干扰滤波和电缆及连接器设计等角度出发，破坏干扰产生的成立条件，从而抑制串扰现象[33]。其中电极的连接方式对信号中引入的串扰分量大小有重要影响。

　　首先在玻纤板上对比使用鳄鱼夹连接与焊接的方式连接薄膜到电路的接口部分所获得的信号，可以观察到激励源与接收位置相同时，使用鳄鱼夹连接和使用焊接连接得到的串扰信号幅值分别为7.487 V和0.4995 V，前者幅值约为后者的15倍，如图9所示。可以观察到鳄鱼夹引入了更大的串扰，这可能是由于鳄鱼夹充当接收天线，会产生大量的感应电流。同时，连接鳄鱼夹的接线端过长会导致屏蔽线缆的屏蔽层失去作用[33]。此外，鳄鱼夹连接还可能会导致夹具与导线脱落、引入寄生电容等不利因素，故实际应用时应选择更加稳定的连接方式[28]。

　　(图9 两种连接方式的串扰信号幅值对比 Fig. 9 Comparison of crosstalk signal amplitude for two connection methods：使用鳄鱼夹连接、使用焊接连接)

　　随后在铝板上对比地线的不同连接方式的效果。当地线松散并未紧贴板面时，其串扰幅值远大于地线用焊锡浸润并贴合板面时的串扰幅值，如图10(a)、(b)所示。这可能是因为松散的地线连接在引入寄生电容和电感的同时，增大了接地电阻，使干扰信号侵入转换电路，从而增加了输出信号的干扰。当传感信号中存在串扰分量时，使用前文所述的两种方法同样可以有效抑制传感信号中的串扰分量，提取出与串扰信号重叠的超声信号，如图10(c)、(d)所示。

　　(图10 铝板测试结果 Fig. 10 Test results in aluminum plate：(a)接地后无串扰的信号;(b)包含串扰分量的信号;(c)移相与差分放大补偿结果;(d)基于互相关的迭代逼近补偿结果)

　　5 结论

　　针对GNP/PVP压阻式薄膜传感器在与超声发射装置近距离工作时所存在的电磁干扰问题，提出了两种有效的传感信号中串扰分量的抑制方法，分别为移相与差分放大补偿方法和基于互相关的迭代逼近方法。通过实验验证和数据分析，两种方法均可提高超声信号的纯净度，大幅抑制在测试过程中传感信号的串扰分量。其中，移相与差分放大补偿方法能够直接输出已抑制串扰的信号，但依赖操作人员的手动调节;而基于互相关的迭代逼近方法虽然处理精度更高(串扰信号区间方差减少99.18%)，但实时性较差。

　　针对电极与导线之间连接方式对串扰幅值的影响，在实际应用中应采用稳定的连接方式(如焊接)并保持良好接地，以避免干扰引入。本文研究成果可为压阻式薄膜超声传感器在复杂电磁环境中的应用提供重要技术支持，有助于提升无损检测结果的精度和检测效率，具有良好的应用前景。

　　参考文献

　　[1] GUPTA M, KHAN M A, BUTOLA R, et al. Advances in ultrasonic non-destructive testing (NDT): Present and future domain[J]. Journal of Research in Engineering and Technology, 2022, 8(2):2286-2307.

　　[2] 金富日. 超声无损检测技术及其在船舶焊接中的应用研究[J]. 中国修船, 2024, 37(S1):28-31. JIN F R. Research on ultrasonic non-destructive testing technology and its application in ship welding[J]. China Ship Repair, 2024, 37(S1):28-31.

　　[3] SHARMA A K. Ultrasonic testing for structural health monitoring of totally-additive carbon composites[C]. Bellingham: SPIE, 2024:243-253.

　　[4] WANG Q, SU Y, SU Y, et al. Manufacturing-driven in-situ monitoring of fiber-reinforced polymer composites: A mechanical engineering perspective[J]. International Journal of Industrial Engineering, 2018, 7(2):42-49.

　　[5] 朱甜甜, 周文彬, 周正干, 等. 曲面构件阵列超声频域逆时偏移成像方法研究[J]. 仪器仪表学报, 2024, 45(6):156-165. ZHU T T, ZHOU W B, ZHOU Z G, et al. Research on array ultrasonic frequency domain reverse time migration imaging method for curved-surface components[J]. Chinese Journal of Scientific Instrument, 2024, 45(6):156-165.

　　[6] 曹欢庆, 朱启民, 赵培含, 等. 复杂型面结构超声成像检测研究进展[J]. 仪器仪表学报, 2024, 45(6):129-138. CAO H Q, ZHU Q M, ZHAO P H, et al. Research progress of ultrasonic imaging detection for complex-shaped structures[J]. Chinese Journal of Scientific Instrument, 2024, 45(6):129-138.

　　[7] 沈建中, 黎连修. 超声无损检测的进展——学会成立20周年回顾[J]. 无损检测, 1998, 20(2):31-33, 38. SHEN J Z, LI L X. Progress of ultrasonic non-destructive testing: Twenty-year review of the Chinese Society for Nondestructive Testing[J]. Nondestructive Testing, 1998, 20(2):31-33, 38.

　　[8] 罗雄彪, 陈铁群. 超声无损检测的发展趋势[J]. 无损检测, 2005, 27(3):148-152. LUO X B, CHEN T Q. Development trends of ultrasonic non-destructive testing[J]. Nondestructive Testing, 2005, 27(3):148-152.

　　[9] 王珅, 王仕强, 伍剑波, 等. 基于柔性阵列压电传感器的页岩气管道壁厚监测[J]. 无损检测, 2022, 44(12):48-53. WANG K, WANG S Q, WU J B, et al. Wall thickness monitoring of shale gas pipeline based on flexible array piezoelectric sensors[J]. Nondestructive Testing, 2022, 44(12):48-53.

　　[10] 沈意平, 翁晶, 刘翊, 等. 基于柔性压电材料传感器的法兰螺栓松动检测[J]. 无损检测, 2022, 44(9):16-21. SHEN Y P, WENG J, LIU Y, et al. Flange bolt looseness detection based on flexible piezoelectric material sensor[J]. Nondestructive Testing, 2022, 44(9):16-21.

　　[11] CHATILLON S, CATTIAUX G, SERRE G, et al. Ultrasonic non-destructive testing with a flexible phased array transducer[J]. Ultrasonics, 2000, 38(1-8):131-134.

　　[12] 钱盛杰, 郭伟灿. 厚壁筒形件内表面径向缺陷检测的超声聚焦技术[J]. 无损检测, 2016, 38(12):55-58, 61. QIAN S J, GUO W C. Ultrasonic focusing technique for radial defects detection of inner surface of thick-walled cylindrical item[J]. Nondestructive Testing, 2016, 38(12):55-58, 61.

　　[13] GUAN R Q, ZOU F, LIAO Y ZH, et al. Highly sensitive strain sensors based on graphene/polymer nanocomposite film fabricated by spray coating[J]. Composites Science and Technology, 2021, 216(37):109079.

　　[14] PAYANDEHPEYMAN M, KHAMEHCHI M. Prediction of electrical conductivity of graphene nanocomposites considering interphase, tunneling effects and geometry[J]. Composites Communications, 2020, 21(5):100364.

　　[15] MAZAHERI M, KHAMEHCHI M. A theoretical model for percolation behavior of exfoliated graphene nanoplatelets/polymer composites[J]. Composites Science and Technology, 2022, 219(8):109843.

　　[16] ZENG H, XU L, LIU M, et al. Ultra-broadband frequency responsive sensor based on lightweight and flexible carbon nanostructured polymeric nanocomposites[J]. Carbon, 2017, 121(55):490-501.

　　[17] WENG X, GUAN R Q, ZOU F, et al. A highly sensitive hybrid carbon nanofillers based sensor for acquiring high-frequency ultrasonic waves[J]. Carbon, 2020, 169(58):403-413.

　　[18] LEE D, LEE H, JEONG Y, et al. Highly sensitive, transparent, and durable pressure sensor based on polydopamine@ urchin shaped metal nanoparticles[J]. Advanced Materials, 2016, 28(42):9364-9369.

　　[19] BI Y, YANG L, LI Z, et al. Highly sensitive piezoresistive pressure sensor based on MXene aerogel for accurate human blood pressure and heart rate monitoring[J]. RSC Advances, 2022, 12(4):2391-2398.

　　[20] CEN-PUC M, DE RIJK T, GLEASON K, et al. All-inkjet-printed flexible carbon nanotubes/polymer nanocomposite pressure sensor[J]. IEEE Sensors Journal, 2021, 21(22):24744-24751.

　　[21] KANG M, LI X, ZHAO X D, et al. Piezo-resistive pressure sensor based on graphene-silver nanocomposite films by blade-coating[J]. Nanomaterials, 2020, 10(8):1524.

　　[22] ZHOU Y ZH, LIAO Y ZH, SU ZH Q, et al. Graphene/polymer nanocomposite for self-sensing ultrasonic guided waves: An experimental and analytical study[J]. Composites Science and Technology, 2020, 197(8):108273.

　　[23] LI M, PAYANDEHPEYMAN M, KHAMEHCHI M. A developed effective medium model for flexible polymer-graphene nanosheet-polymer composites considering tunneling effect on electrical conductivity[J]. Composites Communications, 2022, 13(1):264-275.

　　[24] DUAN X, CAO W, LIAO Y ZH, et al. Towards “sensor-free” structural health monitoring by developing the strain sensor response of composite to ultrasonic guided waves[J]. Composites Science and Technology, 2018, 168(34):203-213.

　　[25] ZHANG F, YANG Y, WANG J, et al. Flexible piezoresistive sensor based on graphene/sponge nanocomposite for human motion monitoring[J]. Journal of Materials Science & Technology, 2022, 107:144-152.

　　[26] SONG P, LIU Q, CHEN L, et al. Compressible MXene aerogel-based highly sensitive pressure sensor as versatile electronic skins[J]. Advanced Functional Materials, 2020, 30(38):20030-20036.

　　[27] GUAN R Q, ZOU F, LIAO Y ZH, et al. Broadband ultrasonic sensor fabricated by atomization-assisted spray coating of GNP/PVP nanocomposite[J]. Advanced Engineering Materials, 2022, 24(11):2000462.

　　[28] 杨阳, 朱峰. 基于容性耦合的钢轨压力传感器电磁干扰分析[J]. 仪器仪表学报, 2024, 45(4):317-324. YANG Y, ZHU F. The electromagnetic interference analysis of rail pressure sensor based on capacitive coupling[J]. Chinese Journal of Scientific Instrument, 2024, 45(4):317-324.

　　[29] 邓江勇, 陈振华, 董德秀, 等. 超声相控阵传感器阵元间串扰源分析及其隔离方法[J]. 电子测量与仪器学报, 2022, 36(9):132-139. DENG J Y, CHEN Z H, DONG D X, et al. Analysis of crosstalk between elements in ultrasonic phased array transducer and its isolation method[J]. Journal of Electronic Measurement and Instrumentation, 2022, 36(9):132-139.

　　[30] 程擎, 但诗芸, 鲁合德. 高压线对机场全向信标及测距仪的电磁干扰分析[J]. 电子测量技术, 2021, 44(18):13-18. CHENG Q, DAN S Y, LU H D. Analysis of electromagnetic interference from high voltage line to omnidirectional beacon and rangefinder in airport[J]. Electronic Measurement Technology, 2021, 44(18):13-18.

　　[31] 孔祥洪, 郭阳雪, 陈国华. 移相器电路分析与仿真[J]. 实验技术与管理, 2013, 30(8):69-73. KONG X H, GUO Y X, CHEN G H. Design and simulation of operational amplifier phase shift circuit[J]. Experimental Technology and Management, 2013, 30(8):69-73.

　　[32] LIU X, ZHANG L, M W, et al. Acoustoelastic theory to an open-source tool for complex waveguides[J]. Ultrasonics, 2024, 136(65):107144.

　　[33] 张伯龙. 电磁兼容(EMC)原理、设计与故障排除实例详解[M]. 北京: 化学工业出版社, 2021.