基于天气状态模式识别的光伏电站发电功率分类预测方法
时间:
摘要:光伏发电功率的准确预测对电网调度的计划安排及光伏电站的优化运行具有重要意义。采用单一模型实现多种不同天气状态下光伏发电功率的准确预测非常困难。在分析辐照度变化规律基础上,综合考虑分类总数、类型代表性和分布均衡性,针对气象专业天气类型进行归纳合并,得到 4 种广义天气类型;进而给出光伏发电功率分类预测的基本框架;提取辐照度的特征参数,建立基于支持向量机的天气状态模式识别模型,辨识恢复部分历史数据所缺失的天气类型信息;最后利用光伏电站的实际运行数据进行仿真,结果验证了模式识别的准确性和分类预测的有效性。
关键词:光伏电站;功率预测;模式识别;太阳辐照度;支持向量机;天气状态
0 引言
在能源消费快速增长和气候环境不断恶化的严峻形势下,推动经济社会的可持续发展,必须大力发展太阳能、风能等新能源。作为太阳能利用的重要方式,近年来光伏发电增长迅速,2012 年全球新增装机容量 28.4 GW,累计达 96.5 GW[1]。截止 2012 年底我国光伏累计装机容量为 7 GW,预计到 2015 年总容量将达 35 GW,未来发展潜力巨大[2]。由于出力的随机波动特性,规模化与分布式光伏的大量接入给电力系统的规划、运行、调度和控制带来巨大挑战。准确的光伏功率预测不仅能够为电网调度决策行为提供依据,还能为多种电源时空互补与协调控制提供支撑,可降低旋转备用容量和运行成本,对保证系统的安全稳定、促进电网的优化运行具有重要意义[3]。
光伏功率预测建模包括物理方法和统计方法,物理方法着眼于从太阳能到电能转化过程中的能量转化装置及控制系统各部分的数学模型,其有效性取决于对研究对象结构及其遵循规律的把握程度和模型参数的精度,涉及环节多、过程复杂、参数求解困难。目前应用较多是神经网络[4-9]、支持向量机(support vector machine,SVM)[10-11]、马尔科夫链[12]等统计方法。
文献[4-6]利用神经网络预测并改进了学习算法,训练样本采用相似日的历史记录;文献[7]按照不同季节分别建立预测子模型,以日类型指数作为输入,但并未给出日类型指数的明确定义;文献[8-9] 分别建立了晴天、多云、阴雨 3 种不同的预测子模型,通过自组织映射和天气预报信息对未来 24 h 的天气类型进行分类或聚类识别;文献[10-11]将历史数据分为 4 种不同的天气类型,利用每种类型各自的历史数据,基于 SVM 分别建立 4 个预测子模型,并根据天气类型预报信息选择对应的模型进行预测;文献[12]采用马尔科夫链预测并针对状态转移矩阵进行了修正。
光伏发电功率受多元气象因素影响,其预测精度与天气状态密切相关[13-14]。上述文献提出的根据不同天气状态分类进行预测的思路,可降低建模难度、简化模型结构,能够有效地提高预测准确性。但针对决定分类建模有效性的 3 个基本问题:天气类型的科学划分、历史数据的完整性以及分类预测方法基本框架的深入研究目前尚未见报道。天气类型的划分是否科学决定了不同天气类型历史数据的分布是否均衡、合理,关系到分类预测是否可行;部分历史数据对应的天气类型信息可能由于传输错误、通信故障、服务中断等原因造成缺失,使得这些数据不能用于分类模型的学习训练,从而影响模型的泛化能力。为此,本文首先在分析辐照度变化规律的基础上,针对气象专业天气类型进行归纳合并,得到 4 种广义天气类型;进而给出了光伏功率分类预测的基本框架;然后建立基于 SVM 的天气状态模式识别模型,对缺失天气类型信息的历史数据进行辨识;最后,利用光伏电站的实际运行数据进行仿真,验证模式识别的准确性和分类预测的有效性。
1 广义天气类型
1.1 地外辐照度
由于大气的吸收、散射和反射,太阳辐射自地外大气层上界经大气层到达地球表面后会有一定衰减。
1.2 广义天气类型
描述天气状态可以有多种不同的方式,例如温度的高低、天空晴朗的程度、降水量的多少等。天气类型作为描述大气物理状态的标签,综合了各种气象因素在时间和空间上的分布,能够比较全面地表征天气状态的特点。中国气象局制订的国家标准 GB/T 22164—2008 将天气状态分为 33 种不同的类型[16]。
地表与地外辐照度之间关系与天气状态的变化密切相关。不同天气类型下大量辐照度数据的统计分析与对比研究表明,晴天、多云、阵雨、大雨是具有典型代表意义的天气类型,这 4 种类型辐照度的变化规律有明显的区别,具有各自鲜明的特点,且这 4 种天气类型出现的几率较高,涵盖了绝大多数日期对应的天气状态。晴天时由于天空遮蔽很少且大气的物理状态比较稳定,所以地表与地外辐照度两条曲线的形状基本一致,两者的变化规律非常接近,相关程度很高。多云时由于部分天空的遮蔽和大气物理状态存在一定波动,所以地表与地外辐照度曲线形状出现较小差异,两者变化规律较为接近,相关程度较高。阵雨时由于大气物理状态的变化,地表与地外辐照度曲线的形状差异明显,两者变化规律的区别较大,相关程度较低。大雨时辐照度衰减严重,地表与地外辐照度曲线的形状完全不同,两者的变化规律区别很大,相关程度很低。
以某光伏电站 2012 年的历史数据为例,这 4 种天气类型辐照度地表实测值与对应地外理论值经归一化后如图 1 所示,两者之间的相关系数 R 也在图中一并给出。
由图 1 可知,地表与地外辐照度的相关系数分别为:晴天 0.997 9;多云 0.864 0;阵雨 0.721 0;大雨 0.437 2。相关性依次降低,与上述分析一致。基于以上分析,可以考虑按照气象专业天气类型分类建模,这样虽然精确性很好但工作量过大,并且那些出现概率很低的天气类型所对应的历史记录很少甚至空白,这会使所建对应模型的性能无法保证甚至根本无法建模。
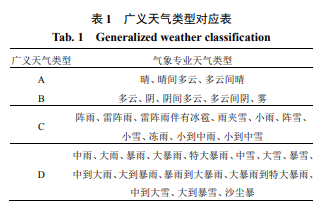
综上所述,为实现科学的分类预测,需要遵循以下 3 个基本原则。第一,兼顾精确性与建模难度及复杂性,即分类总数既不能太多也不能太少,分类太多则建模过于复杂、工作量大,分类太少则对天气状态的描述不够细致,达不到提高预测精度的效果。第二,对应不同天气状态的类型应具有典型性和代表性,有明确的物理意义,保证分类建模的合理性。第三,为保证建模可行性和精度,针对已有的历史记录,要尽量使样本数据在不同类型上的分布较为均衡。为此,在综合考虑上述原则基础上,以前文所述 4 个典型天气类型为代表,分别建立 A、 B、C、D 4 个子集,按照相似程度从高到低(即地表与地外辐照度相关系数从大到小)的顺序和历史数据在各子集中尽量均衡分布原则,将所有气象专业天气类型均依次顺序合并到这 4 个子集中,每个子集均包含不止一个气象专业天气类型,这些子集称为广义天气类型,其与 33 个气象专业天气类型之间的对应关系如表 1。
需要说明的是,不同光伏电站所积累的历史数据中各种气象专业天气类型的分布存在差异,同一个气象专业天气类型在不同地域光伏电站的历史数据中的分布也有差别。因此,在定义广义天气类型时不宜设定统一不变的固定标准,而应在综合考虑 3 个基本原则基础上,结合不同地域的气象特点,以相关系数和辐照度的数值大小为参考,根据历史数据的具体分布情况来确定。
2 光伏发电功率分类预测方法
分类预测涉及的天气类型信息有 2 种,第一种是光伏电站历史数据中所包含的实际天气类型信息,此信息决定了历史数据对应的天气类型分组;第二种是针对预测日(第 2 天)天气类型的预报信息,通常由气象专业服务机构提供,据此信息确定使用哪类模型进行预测。在获取这 2 类信息的基础上,本文提出光伏发电功率分类预测方法的基本框架,如图 2 所示。
对于大部分历史数据,其记录中应包含该日对应的天气类型信息,但在实际中往往由于某种原因造成历史数据对应天气类型信息的缺失,如通信故障、服务中断、存储错误等。在分类建模时,只有具有完整天气类型信息的历史数据才能用于分类建模,而缺失天气类型信息的历史数据无法用于模型的学习训练,这可能导致预测模型性能的降低甚至建模困难。为此,需要提取历史数据中能够反映天气类型特点的特征,建立天气状态模式识别模型,对缺失类型信息的历史数据进行辨识恢复。地表辐照度与天气类型密切相关,当天气状态发生变化时地表辐照度会出现突变,但对应的地外辐照度并不受天气状态影响而依然保持其固有的变化规律,因此,可以通过地表与地外辐照度之差(简称辐照度差)来描述天气状态的变化。
3 辐照度的特征提取
3.1 总体统计特征
3.1.1 晴朗指数
晴朗指数定义为地表与地外辐照度一天之内的曝辐量之比,离散采样情况下曝辐量为相邻采样值围成梯形的面积,在地表与地外辐照度采样间隔相同的条件下,晴朗指数可按式(2)计算。
3.1.4 辐照度差三阶导数
从数学角度来说,导数对应变化率,因此,辐照度差对时间的导数能反映其变化率的大小。由于辐照度为离散数据,所谓导数实为差分,为符合习惯本文依然称之为导数。前期的研究结果表明[17],辐照度差的各阶导数与天气状态的波动程度均正相关,当天气状态发生快速变化和剧烈波动时,三阶导数明显大于其它阶导数,其对天气状态快速变化的敏感程度高于其它阶导数。
相关知识推荐:光伏发电技术应用论文发表什么期刊
当相邻两个采样时刻的辐照度数值相等时,此时段对应的趋势指标 fi(Gs,i,G0,i)为零,对不一致性系数没有影响。Knc为全部采样时段的趋势指标之和,可作为地表与地外辐照度变化趋势一致性的度量指标,其数值越大,说明两者变化趋势越不一致,反之则表示变化趋势越一致。 4 天气状态模式识别模型 4.1 SVM 基本原理 SVM 是基于结构风险最小化的统计学习方法,综合考虑了经验风险和置信区间,能够兼顾训练误差和泛化能力[18-19],其性能优于人工神经网络等传统的学习方法,在电力系统的负荷预测、故障识别、稳定评估等领域有着广泛应用。
4.2 基于 SVM 的天气状态模式识别模型
前文介绍的 SVM 只考虑了两分类问题,对多分类问题则需构造多分类器,主要方法有 2 种。第一种是“一对多”方式,即一个分类器将每一类型与其它类型分开,对于 K 类问题需要构造 K 个分类器,第 i 个分类器用第 i 类的训练样本作为正的训练样本,用其它类样本作为负的训练样本,此方式的缺点是训练样本数大,训练困难,推广误差无界。第二种是“一对一”方式,即在 K 类训练样本中构造所有可能的两分类器,共需构造 K(K− 1)/2 个分类器,每类仅在 K 类中的 2 类训练样本上训练,使用投票法决定样本所属的类,此方式的缺点是推广误差无界,分类器数目随类数急剧增加。为缩短学习训练的时间,本文采用“一对一”方式。
5 仿真与分析
5.1 实验数据
为验证本文模式识别模型和分类预测方法,利用内蒙古某光伏电站实际运行数据,采用 Matlab 7.12 和 LIBSVM 编程进行仿真[20]。历史数据时间范围为 2012 年 1—12 月,采样间隔为 30 min,有效记录 310 天,地表辐照度实测值曲线如图 3 所示。
5.2 天气状态识别模型
仿真 SVM 选择高斯核函数,选择 K= 3,对 SVM 模型进行优化,以分类误差最小为评价指标,惩罚系数和核函数参数设置的变化范围为 2−10~210,优化后得到惩罚系数 C为69 644,高斯核函数参数为4。
历史数据记录的广义天气类型分布见表 2。将所有的样本数据分为 2 组,第 1 组占样本总数的 70%,作为训练集,第 2 组占样本总数的 30%,作为测试集。SVM 天气状态模式识别模型分类结果的混淆矩阵见表 3。
测试集中分类正确和错误的天数分别在表 3 的对角线和其他位置给出,分类的整体精度(overall accuracy,OA)为 94.62%,这表明模型的输入特征量能反映不同广义天气类型的特点,SVM 分类模型的总体识别精度较好。
5.3 分类预测方法仿真
首先采用神经网络建立一个统一预测模型,然后按照图 2 方法针对 4 种广义天气类型分别建立 4 个对应的预测子模型,利用光伏电站的实际数据进行仿真。2 种方法在 B、C 天气类型下的预测值与实测值如图 4。
5.4 分析讨论
光伏发电功率预测模型的数学本质是在高维空间中建立历史数据与未来发电功率之间的映射关系。由于不同天气状态下辐照度、发电功率的变化规律有明显区别,利用单个模型拟合如此分散的映射关系非常困难。因此,统一的预测模型对于多变天气状态难以取得理想效果。
本文提出的广义天气类型既对不同天气状态进行了合理区分和定性描述,也保证了历史数据在不同类型中的均衡分布,确保分类建模能够顺利实施;针对不同天气类型分别采用对应模型对其映射关系进行拟合的分类预测方法可降低建模难度,增强各子模型的泛化能力,从而提高多变天气状态下光伏发电功率的预测精度。
6 结论
基于天气状态模式识别的分类预测方法利用同类的样本数据针对不同状态分别建模,能够提高模型精度和预测准确性。文章给出光伏发电功率分类预测的基本框架,建立了相应的辨识模型以提高样本数据的完整性,对于实际光伏功率预测系统的开发有着重要的指导意义和应用价值。
为进一步提高光伏发电功率分类预测的准确性,今后需针对以下问题开展进一步研究:
1)天气类型的科学划分问题,这需要对气象要素的变化规律进行深入分析,同时还要考虑对不同样本数据分布情况的适应性和分类预测模型总数的限制。
2)在上述基础上研究能够准确反映不同天气状态特点的气象要素特征提取问题,以及适合分类识别的机器学习方法。——论文作者:王飞 1 ,米增强 1 ,甄钊 1 ,杨光 1 ,周海明 2
参考文献
[1] International Energy Association Photovoltaic Power Systems Programme (IEA PVPS).IEA PVPS annual report 2012[EB/OL].Fribourg:IEA PVPS,(2013-04-30) [2013-5-19].http://iea-pvps.org/index.php?id=6&no_cache= 1&tx_damfrontend_pi1%5BshowUid%5D=1129&tx_dam frontend_pi1%5BbackPid%5D=6.
[2] 中华人民共和国国务院.国务院关于促进光伏产业健康发展的若干意见[EB/OL].北京:国务院,(2013-07-15) [2013-07-19].http://www.gov.cn/xxgk/pub/govpublic/mrlm/ 201307/t20130715_66188.html. The Central People’s Government of the People’s Republic of China. Several opinions on promoting the healthy development of photovoltaic industry[EB/OL]. Beijing:The Central People’s Government of the People’s Republic of China , (2013-07-15)[2013-07-19] . http://www.gov.cn/xxgk/pub/govpublic/mrlm/201307/t2013 0715_66188.html (in Chinese).
[3] Eltawil M A,Zhao Z.Grid-connected photovoltaic power systems:technical and potential problems-a review[J]. Renewable and Sustainable Energy Reviews,2009,14(1): 112-129.
[4] İzgi E,Öztopal A,Yerlib B,et al.Short-mid-term solar power prediction by using artificial neural networks[J]. Solar Energy,2012,86(2):725-733.
[5] 丁明,王磊,毕锐.基于改进 BP 神经网络的光伏发电系统输出功率短期预测模型[J].电力系统保护与控制, 2012,40(11):93-99,148. Ding Ming,Wang Lei,Bi Rui.A short-term prediction model to forecast output power of photovoltaic system based on improved BP neural network[J].Power System Protection and Control,2012,40(11):93-99,148(in Chinese).
[6] 王飞,米增强,杨奇逊,等.基于神经网络与关联数据的光伏电站发电功率预测方法[J].太阳能学报,2012, 33(7):1171-1177. Wang Fei,Mi Zengqiang,Yang Qixun,et al.Power forecasting approach of PV plant based on ANN and relevant data[J].Acta Energiae Solaris Sinica,2012, 33(7):1171-1177(in Chinese).
[7] 陈昌松,段善旭,殷进军.基于神经网络的光伏阵列发电预测模型的设计[J].电工技术学报,2009,24(9): 153-158. Chen Changsong,Duan Shanxu,Yin Jinjun.Design of photovoltaic array power forecasting model based on neutral network[J].Transactions of China Electrotechnical Society,2009,24(9):153-158(in Chinese).
[8] Chen Changsong,Duan Shanxu,Cai Tao,et al.Online 24-h solar power forecasting based on weather type classification using artificial neural network[J].Solar Energy,2011,85(11):2856-2870.
[9] 代倩,段善旭,蔡涛,等.基于天气类型聚类识别的光伏系统短期无辐照度发电预测模型研究[J].中国电机工程学报,2011,31(34):28-35. Dai Qian,Duan Shanxu,Cai Tao,et al.Short-term PV generation system forecasting model without irradiation based on weather type clustering[J].Proceedings of the CSEE,2011,31(34):28-35(in Chinese).
[10] Shi Jie,Lee Weijen,Liu Yongqian,et al.Forecasting power output of photovoltaic systems based on weather classification and support vector machines[J] . IEEE Transactions on Industry Applications,2012,48(3): 1064-1069.


