轮轨接触几何非线性对车辆动力学性能的影响
时间:
摘要:为探究轮轨接触几何非线性与车辆动力学性能的关系,提出一种新的轮轨接触几何非线性参数,即复合等效锥度,讨论伴随车轮磨耗增加,复合等效锥度对车辆动力学性能的影响。以线性等效锥度为基础,通过不同轮对横移量对应的接触宽度差值占比对线性等效锥度进行加权,得到复合等效锥度。实测磨耗车轮型面,对比随运营里程增加不同轮轨接触几何参数的变化规律。基于 UM 建立车辆动力学模型,讨论轨道不平顺激励下复合等效锥度与车轮磨耗之间的关系以及对车辆动力学性能的影响。研究结果表明:复合等效锥度考虑了轮轨接触几何状态变化,计算时不受轮对大位移时局部磨耗的影响,可以更真实地反映轮轨接触的非线性状态。与等效锥度相比,中低不平顺激励下复合等效锥度对轨道不平顺的大小更敏感。复合等效锥度与车辆动力学性能之间存在明确的对应关系。随着复合等效锥度增加,车辆稳定性下降。当复合等效锥度超过 0.29 后,车辆动力学性能指标的变化趋于稳定。通过复合等效锥度,可对线路不平顺等级和车辆动力学性能进行评估,对轨道车辆设计与维护有一定指导意义。
关键词:轮轨关系;接触几何非线性;等效锥度;车轮磨耗;动力学指标
京津城际铁路、哈大线、哈齐线出现过多次高速动车组转向架失稳以及由此产生的运行品质和安全性问题。车辆出现失稳时,轮轨间会产生强烈的相互作用,加剧轮轨磨耗或疲劳,对线路造成严重破坏甚至引起车辆脱轨事故。轮轨关系是车辆系统动力学性能的决定因素,其好坏不仅取决于轮轨的截面外形,还受到轨距、轨底坡、轨道在垂向横向上的不平顺以及铁轨柔性支撑等因素的影响。轮轨接触几何是指车轮与钢轨接触的几何状态,其对车辆运行品质和曲线通过等方面有着重大影响,是讨论轮轨关系的重要组成部分。在轨距等参数相对固定的情况下,轮轨型面匹配下的几何接触也就成为研究轮轨关系的主要问题。早期对于轮轨接触几何的研究往往从线性参数的角度入手,然而非线性铁道车辆系统动力学的研究表明非线性轮轨关系对车辆运行状态有非常重要的影响。因此对高速列车在长期服役过程中的轮轨接触几何非线性参数和车辆动力学性能之间关系的研究显得尤为必要。国内外诸多学者对此展开研究。POLACH [1-3]基于实测车轮型面数据,提出非线性轮轨接触 NP 参数, 分析了不同磨耗轮轨型面匹配下临界速度的变化。许自强[4]提出了车轮镟修后初始等效锥度限制,得出了根据等效锥度限值对车轮进行管理可以控制轮轨型面与接触关系。刘付山等[5]考虑轮轨接触几何非线性计算不同轨道谱和车辆运行速度下车辆-轨道-桥梁垂向耦合系统的随机振动。许贵满等[6]建立轮轨三维实体非线性接触模型,探究在轮轨高低不平顺下曲线超高对轮轨非线性接触系统的动力影响。PARK 等[7]运用分岔理论分析了非线性临界速度,通过计算非线性动态车辆模型的极限环来研究铁道车辆的横向稳定性。TRUE 等[8]引入“相空间”来说明非线性动力学系统,讨论了多平衡态的重要情况及其对参数的依赖关系。梁树林等[9]结合抗蛇行减振器与轮轨型面匹配对车辆非线性稳定性进行分析,探究影响非线性稳定性的因素。董孝卿等[10]引入非线性因子对名义等效锥度进行修正,提出非线性等效锥度𝜆𝐺这一新参数。上述研究表明从研究轮轨接触几何非线性参数计算方法以及车辆运行非线性稳定性具有实际意义。然而,对轮轨接触非线性参数的推导往往仅从单一线性参数展开,例如等效锥度,无法反映轮轨接触区域的变化情况。本文首先从线性等效锥度、轮轨接触区域参数引出新的轮轨接触几何非线性参数。然后建立车辆动力学模型,讨论不同轮轨不平顺下车轮磨耗与新参数的关系,最后结合车轮磨耗讨论新参数与车辆动力学指标之间的关系。本文提出的新参数可有效的描述轮轨接触非线性特性,为轮轨接触几何非线性研究提供一种新思路。
1 非线性轮轨接触参数提出、介绍
1.1 线性等效锥度
同一轮对左右车轮的滚动圆半径之差定义为轮径差,在一定的横移量范围内,轮对的轮径差与其相对钢轨的横移量之间为直线关系,该直线的斜率定义为等效锥度𝜆𝑒。等效锥度在铁路行业中应用广泛,它反映轮对的直线稳定性和曲线通过性能,例如在直线上运行时,等效锥度决定列车的对中性能和轮轨的匹配程度,以及运行稳定性等性能。在轮轨线性特性中,通常用轮对横移 3 毫米处的等效锥度(名义等效锥度)来描述轮轨接触几何特性。
2 车轮磨耗对非线性参数的影响
2.1 实测车轮型面分析
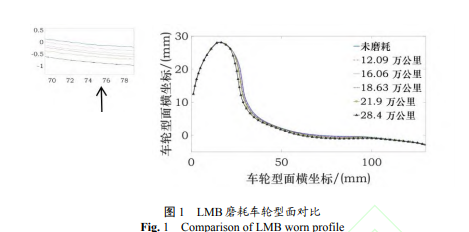
由于在车辆在运行过程中车轮与钢轨之间存在相互作用,车轮踏面出现磨耗,轮轨接触几何状态也随之发生改变。本节通过实测车轮型面和仿真计算探究车轮磨耗与复合等效锥度的关系。基于某既有线路上高速运行的 CRH3 动车组(LMB 车轮与 60 轨)进行追踪测试,得到车辆运行 12.09、16.06、18.63、21.9、28.4 万公里的轮对右轮踏面的型面如图 1。
从图 1 可以看出,早期的车轮磨耗主要发生在低锥度的轮对小位移区域,以踏面磨耗为主,随着车辆运营里程的增加,车轮踏面磨耗速度加快,表现为图 1 的局部放大图中车轮型面间距随里程的增加而增大。同时车轮磨耗不仅发生在低锥度区,而且发生了轮缘磨耗,磨耗更为严重,这与文献[11]中实测车轮磨耗情况一致。文献[11]中对某列动车组轮对磨耗情况进行了追踪测试,发现在运营里程较小时,踏面出现轻微磨耗,随着运营里程的增大踏面磨耗加剧,当运营里程达到 26.2 万公里后踏面磨耗情况非常严重,并且轮缘磨耗也很明显。
利用 MATLAB 编写程序,对实测车轮踏面的型面进行处理,图 2 为轮轨接触区域参数随磨耗变化的对比图。图 2(a)展示了接触点位置变化率,当轮对横移量较小时,各车轮磨耗状态下接触位置变化率均达到最大值。当轮对从初始位置右移时,各车轮磨耗状态下接触变化率随横移量变化很小,参数取值范围较为集中。当轮对从初始位置左移时,参数取值随横移量变化波动明显,参数取值范围较为分散。可以看出,车轮向车轴中心一侧横移时,磨耗对于接触位置变化率的影响较大。图 2(b)展示了接触宽度变化,可以看出,随着运行里程的增加,轮对横移量为 3mm 时的接触带宽先增加再减小,整体呈现增大的趋势。图 2(c)展示了轮轨接触带宽变化率,在轮对横移量小于 5 mm 时,与新轮相比,车轮磨耗会导致接触带宽变化率急剧增大。当轮对横移量大于 8 mm 时,车轮磨耗对于接触带宽变化率的影响很小,曲线几乎重合,此时新轮的接触带宽变化率明显高于磨耗轮。结合图 2(b)可以看出,随着车辆运营里程的增加,虽然接触宽度会增加,但同时接触点位移的变化更大,导致接触带宽变化率曲线为减函数。
通过编写 MATLAB 程序计算得到复合等效锥度。图 3 为轮轨接触几何线性与非线性参数随磨耗变化的对比。由图 3 可知,随着车辆运营里程的增大,车轮型面磨耗加剧,复合等效锥度𝜆𝑛随之增大。复合等效锥度对于名义等效锥度𝜆e有一个修正,弥补了等效锥度对于非线性轮轨接触表述不足的特点。与等效锥度相比,在整体变化趋势一致的前提下,复合等效锥度𝜆𝑛对于轮对横移量 3mm 附近轮轨接触几何状态随运营里程增长的变化表现得更细致。复合等效锥度𝜆𝑛对于轮对横移量 3mm 附近轮轨接触几何状态随运营里程增长的变化表现得更细致。有前文分析可知,轮对横移量 3mm 时接触宽度随运营里程的增加呈现先增大后减小的整体上升趋势,这意味着𝜆2的权重增大和𝜆4的权重减小,结合复合等效锥度𝜆𝑛相较于名义等效锥度𝜆𝑒先减小后增大的情况可知:𝜆4 − 𝜆2先大于 0 后小于 0,这与文献[1]中所提出 NP 参数的变化规律保持一致。在车辆运行里程大于 18 万公里时,非线性等效锥度𝜆𝐺和复合等效锥度𝜆𝑛对于名义等效锥度值都有正向修正,对于非线性轮轨接触的状态可以视为有相同的描述。
2.2 仿真车轮磨耗分析
在车辆动力学软件 UM 中,建立 50 自由度的 CRH380B 车辆动力学模型,包括 1 个车体、2 个构架、 4 个轮对、8 个轴箱、一系和二系悬挂。其中车体、构架和轴箱均设为刚体,分析中不考虑其弹性变形[12]。模型将弹簧、减振器、横向止挡、牵引拉杆和抗侧滚扭杆简化为特定类型的作用力(图 4)。实际上采用柔性车体可以得到更接近实际情况的结果[13],为了简化计算,本文仍选择刚体模型。
基于上述车辆动力学模型,轮轨型面设为 LMB 与 60 轨,以武广线实测不平顺作为输入,全长 7000 米,通过计算车体横向振动并与实测结果对比进行模型的验证。将车体横向振动加速度的仿真数据与试验数据进行 PSD 变换后在频域范围内的对比如图 5 所示。从图 5 可以看出,仿真计算的振动主频为 2.1484,试验测量的振动主频为 2.1469。仿真与试验存在一定误差的主要原因是:仿真计算中车辆系统的输入仅为轨道不平顺,实际车辆在运行过程中还存在很多激扰,例如车辆质量偏心、风阻、车辆各部件间的摩擦等,仿真计算时未考虑上述因素对车辆系统的影响。在误差范围内,仿真与试验所得车体横向振动加速度结果较为吻合,说明建立的车辆动力学模型较为可靠,在后续研究中通过该模型得到的车辆动力学指标在误差范围内满足要求。
基于建立的车辆动力学模型,轮轨匹配选择 LMB 踏面与 CHN60 钢轨,轮轨接触模设为 KikPiotrowski 模型,分别设置从低到高的四个级别的轨道不平顺,线路平面的组合和不同路段的车速依据文献[14-15]设置,选择 Archard 模型模拟车轮磨耗,磨耗系数设为 1.83×10-13,车辆运行总里程设置 30 万公里。图 6(a~d)为各级不平顺下等效锥度与复合等效锥度随运营里程的变化情况。在激励较低时,二者都随着运营里程的增加而增大,此时踏面磨耗表现为凹形磨耗,如图 6(a~b),这与图 3 的实测车轮的情况一致。随着不平顺激励的继续增加,踏面磨耗区域扩大,踏面在磨耗初期产生凹形磨耗,参数值上升明显,随着车辆继续运行,踏面接触区域整体被磨平,参数值趋于平稳,如图 6(c)。当轨道不平顺过大时产生轮缘磨耗,踏面整体被磨平,参数值持续下降,如图 6(d)。图 7 反映出的计算结果与文献[16]的结论相符。可以看出,在不同等级的轨道不平顺激励下,复合等效锥度与等效锥度的变化趋势几乎一致,但复合等效锥度对轮轨不平顺大小更为敏感,复合等效锥度的数值变化更容易反映轨道不平顺大小和车轮磨耗情况。
从图 6 还可以看出,在未产生轮缘磨耗时,轨道不平顺越大,复合等效锥度与等效锥度相差越大。当产生轮缘磨耗后,复合等效锥度与等效锥度数值接近。当车辆在轨道不平顺条件较好的轨道上运行时,采用复合等效锥度更能反映轨道不平顺大小和车轮磨耗情况,当已知轨道不平顺条件较差时,采用名义等效锥度即可满足对轮轨接触几何描述的需求。在评估轨道不平顺大小时,可利用装备相近磨耗程度车轮的车辆运行相同里程后型面复合等效锥度与等效锥度差值的大小给出初步评估。
3 非线性轮轨接触参数对车辆动力学性能的影响
通常对车辆动力学性能的描述主要从:稳定性、安全性和平稳性三个方面进行,其中稳定性常用临界速度和构架横向加速度 RMS 值作为评价指标,安全性常用脱轨系数和轮重减载率作为评价指标,平稳性常用 Sperling 指标和舒适度指标作为评价指标。基于在 UM 中建立的车辆动力学模型,轮轨蠕滑力模型设为 FASTSIM 模型,轨道工况设为直线,轨道不平顺度设为 UIC-good-1000m。采用第二节中 LMB 原形与实测磨耗车轮与 CN60 钢轨匹配,车速设置为 200~350km·h-1,计算车辆动力学性能指标。
仿真计算结果如图 7 所示。图 7(a~h)为车辆稳定性、安全性和平稳性指标与复合等效锥度的关系。由图 7(a)可以看出,随着复合等效锥度的提升,车辆的临界速度呈下降趋势,在 0.33 到 0.36 阶段临界速度出现小幅波动的情况。由图 7(b)可以看出,随着复合等效锥度的增加,临界速度的变化速率呈现“快-慢快”的趋势。在复合等效锥度区 0.27 时,临界速度变化达到最快。复合等效锥度增大反映出轮轨接触类型发生变化以及随之改变的轮轨接触区域参数,同时也反映出磨耗导致轮轨接触点锥度增大,临界速度从而也随之下降。由图 7(c)可以看出,随着复合等效锥度的增大,构架横向加速度 RMS 值先增大后趋于稳定,在复合等效锥度大于 0.29 时,车速 200~250 km·h-1 对应的构架加速度 RMS 值小幅平稳上升,车速 300~350km·h-1对应的构架加速度 RMS 值小幅平稳下降。由图 7(d)可以看出,不同车速下脱轨系数随复合等效锥度的变化规律一致,随着复合等效锥度的增大,脱轨系数先减小后增大。在复合等效锥度大于 0.29 后,脱轨系数小幅波动趋于平稳。由图 7(e)可以看出,随着复合等效锥度的增大,轮重减载率几乎无波动。轮重减载率仅在车速 300km·h-1复合等效锥度接近 0.3 时出现突变,接近车速 350km·h-1对应的数值。轮重减载率与车轮型面关系较小。由图 7(f)可以看出,随着复合等效锥度的增大,车体横向 Sperling 指标呈现“慢-快-慢”的上升趋势,车辆横向平稳性下降。由图 7(g)可以看出,与轮重减载率变化规律相似,车体垂向平稳性几乎不随复合等效锥度变化而变化。由图 7(h)可以看出,与车体垂向平稳性指标变化规律相似,舒适度指标几乎不随复合等效锥度变化而变化,这是因为舒适度指标的垂向加权考虑了较多垂向高频振动。
从上述分析可以看出,复合等效锥度与车辆动力学指标之间存在明显的对应关系,复合等效锥度越大,临界速度越小、构架横向加速度 RMS 值、脱轨系数和车体横向平稳性指标越大,而轮重减载率、车体垂向平稳性指标和舒适度指标变化不明显。可以得出车辆的安全性、稳定性和平稳性随着复合等效锥度增大而降低。在车辆动力学分析中,可以通过复合等效锥度的数值对车辆的动力学性能进行一个初步评价。例如,当车辆系统的某一参数在一定范围内变化时,选取相同线路和轮轨匹配条件,计算达到指定里程后车轮型面的复合等效锥度,判定该参数对车辆动力学性能的影响。
4 总结
1) 相较于已有的轮轨接触非线性参数,复合等效锥度考虑了轮轨接触区域参数的变化,更细致的反映了接触区域的变化情况。随着车轮磨耗的增加,复合等效锥度呈现出与名义等效锥度相同的变化规律:二者都随着磨耗的加剧而增大,此外复合等效锥度的数值变化更容易反映轨道不平顺大小和车轮磨耗情况。
2) 复合等效锥度与车辆稳定性、安全性和平稳性评价指标之间存在明显的对应关系。整体上复合等效锥度越大,车辆动力学性能指标越差。复合等效锥度数值较小时,车辆动力学性能指标变化幅度较大。复合等效锥度数值较大时,车辆动力学性能指标变化幅度较小。
3) 复合等效锥度较为直观地反映轮轨接触几何状态和车辆动力学性能。后续可以以此参数进行车轮型面优化设计等方面的研究。——论文作者:张海 1, 2,冉祥瑞 1,蔡家祺 1,林凤涛 1,王秀刚 2
参考文献:
[1] POLACH O, NICKLISCH D. Wheel/rail contact geometry parameters in regard to vehicle behaviour and their alteration with wear[J]. Wear, 2016, 366/367: 200-208.
[2] POLACH O. Influence of locomotive tractive effort on the forces between wheel and rail[J]. Vehicle System Dynamics, 2001, 35(suppl): 7-22.
[3] POLACH O. Characteristic parameters of nonlinear wheel/rail contact geometry[J]. Vehicle System Dynamics, 2010, 48(suppl): 19-36.
[4] 许自强. 基于动车组横向稳定性的等效锥度限值研究[J]. 中国铁路, 2017(12): 29-34. XU Ziqiang. Research on limit value of equivalent conicity based on lateral stability of EMU trains[J]. China Railway, 2017(12): 29-34.
[5] 刘付山, 曾志平, 郭无极, 等. 考虑轮轨非线性接触的车辆-轨道-桥梁垂向耦合系统随机振动分析[J]. 振动工程学报, 2020, 33(1): 139-148. LIU Fushan, ZENG Zhiping, GUO Wuji, et al. Random vibration analysis of vehicle-track-bridge vertical coupling system considering wheel-rail nonlinear contact[J]. Journal of Vibration Engineering, 2020, 33(1): 139-148.
[6] 许贵满, 韩海娅, 吴亚平, 等. 轮对-曲线轨道非线性接触系统垂向振动分析[J]. 石家庄铁道大学学报(自然科学版), 2021, 34(1): 29-36. XU Guiman, HAN Haiya, WU Yaping, et al. Vertical vibration analysis of wheel-curved track nonlinear contact system[J]. Journal of Shijiazhuang Tiedao University (Natural Science Edition), 2021, 34(1): 29-36.
[7] PARK J H, KOH H I, KIM N P. Parametric study of lateral stability for a railway vehicle[J]. Journal of Mechanical Science and Technology, 2011, 25(7): 1657-1666.
[8] TRUE H. On the theory of nonlinear dynamics and its applications in vehicle systems dynamics[J]. Vehicle System Dynamics, 1999, 31(5/6): 393-421.
[9] 梁树林, 朴明伟, 张祥杰, 等. 高速车辆横向稳定性的非线性影响因素研究[J]. 铁道学报, 2009, 31(5): 23-30. LIANG Shulin, PIAO Mingwei, ZHANG Xiangjie, et al. Investigation of non-linear effects on high-speed vehicle lateral stability[J]. Journal of the China Railway Society, 2009, 31(5): 23-30.
[10] 董孝卿, 任尊松, 许自强, 等. 等效锥度曲线非线性特性及影响研究[J]. 铁道学报, 2018, 40(11): 91-97. DONG Xiaoqing, REN Zunsong, XU Ziqiang, et al. Research on nonlinear characteristics and effect of equivalent conicity curve[J]. Journal of the China Railway Society, 2018, 40(11): 91-97.

 >
>