储层物性的地震预测技术综述

发布时间：2022-01-22

　　摘 要 想要掌握储层物性的空间分布情况，地震预测是不可或缺的手段. 近半个世纪期间，主要出现了 7 种有关储层物性地震预测的方法技术，包括阻抗反演技术、储层物性间接反演技术、储层物性波动方程反演技术、地质统计方法和人工智能预测方法，以及以上方法技术所依赖的机理性岩石物理分析技术和统计岩石物理分析技术，本文论述了这些方法技术的原理及现状. 从反射地震数据出发反演得到地层的声阻抗和弹性阻抗，这已经是石油工业界常规的技术流程. 借助理论和实验手段进行机理性岩石物理分析，进而经由储层物性和阻抗间的媒介关系进行储层物性的间接反演或是基于波动方程进行直接反演，这是进行储层表征的有效途径. 另外，地质统计方法和人工智能方法在储层物性的空间展布预测方面正发挥着独特的作用. 很多情况下，简化物理模型难以描述复杂的动力学机制，而综合了岩石物理理论、随机模拟和 Bayes 估计的统计岩石物理分析技术是另外一种可供选择的储层物性预测方法. 同时，本文也客观地指出了每种预测技术的优点、适用性和局限性，以便读者可以迅速掌握各种技术手段的精髓，并在工作中能够选用适合自己任务特点的储层物性地震预测技术.

　　关键词 地震预测; 储层物性; 岩石物理; 人工智能

　　0 引 言

　　在石油地震勘探开发领域，地震反射波法占据着主导地位( Ashcroft，2011; 威廉·艾思克罗夫特，2017) . 依靠地震反射信息进行地质构造解释已经取得了辉煌的成功，时至今日仍是地震勘探开发领域的基石( Bacon et al. ，2007; 培根等，2013) . 然而，地质目标的日益复杂化对地震技术提出了更高的要求，不仅需要通过高密度高分辨率的地震数据刻画出精细的构造细节，而且还要对储层的物理性质进行可靠地地震表征( Nanda，2016; 尼兰吉安·南达，2019) . 其中，地震反演技术是进行储层表征的主要方法，包括简单的叠后反演技术和更精细的叠前反演技术，从中可以得到诸如储层的岩性、孔隙度、所含流体类型及黏度、流体饱和度、非均质性特征、渗透率等地质参数以及岩石脆性和总有机质含量等石油工程参 数 ( Harvey，1993; Castagna and Smith，1994; Chen and Sidney，1997; Goodway et al. ，1997; Chopra and Marfurt， 2005; 杨培杰，2018) . 在过去几十年的石油勘探开发实践中，地震反演技术展示出了强大的功能，不仅学术界在推动地震反演技术的进步，而且石油工业界已经将此作为了常规生产技术而使其得到了广泛的应用( Pride et al. ，2003; 张明振， 2016) . 尽管地震反演技术不可避免地也存在着自身的诸多局限性，但是它正发挥着无可代替的作用，21 世纪以来一直是地震勘探开发领域的热点.

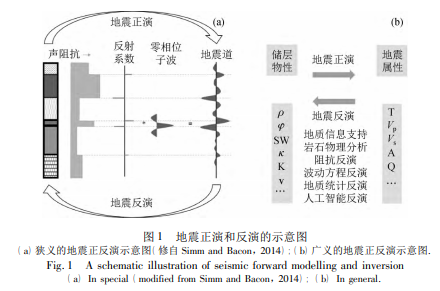
　　地震波在地面或海面被激发后向地下传播，遇到地层界面时被反射回来，反射波具有特定的波形、接收时间、振幅和相位等属性，地震反演正是利用了这些属性，从中推测地层的各种物理性质参数( Barclay et al. ，2008) . 当地层界面两侧的岩性具有差异时，确切地说，存在阻抗差的时候才会产生反射波. 阻抗是地层的物性参数，被定义为地层岩石波速和密度的乘积. 利用测井数据可以得知各个地层的阻抗值，井间区域则需要利用地震信息进行反演求取，除了最基本的阻抗参数之外，有了测井信息和岩石物理分析的帮助，还可以反演出诸多其他的物性参数. 反演是正演的逆过程，如图 1 所示. 已知地质模型的各项构造和岩性参数，求取地震响应的过程就是地震正演. 已知地震记录结果，反推出地质参数的过程就是地震反演( Brown，2011; Latimer，2011; Simm and Bacon，2014) . 在图 1a 中，如果已经由测井得到了声阻抗模型，那么就可以进行正演，将其与地震子波进行褶积就可以得到合成地震响应( 此处为一维地震道) . 地震反演是根据已经记录到的地震响应，利用反褶积去除掉子波的影响而得到地质模型( 此处为声阻抗) . 图 1b 给出了广义地震反演的示意图，即从地震属性( 反射时间 T、纵波速度 Vp、横波速度 Vs、振幅 A 和衰减 Q) 进行储层物性( 地层密度 ρ、孔隙度 φ、含水饱和度 sw、渗透率 κ、体积模量 K 和泊松比 ν 等) 的预测过程.

　　20 世纪 90 年代，以阻抗反演为代表的地震反演技术大量涌现了出来，虽然也依赖于井数据的支持，但一般不涉及过多的岩石物理分析，能够划分出储层和非储层往往也就完成了任务. 另外，地震反演在提高储层分辨率方面也是具有一定 效 果 的 ( 张 永 刚，2002; Latimer，2011; 撒 利 明 等， 2015) .

　　进入 21 世纪，生产实践对地震预测技术的要求升级了，地质学家和地球物理学家期望得到储层的各项物性参数，这就需要从实验和理论两方面进行大量深入的岩石物理分析，以便将地震响应结果与储层物性参数挂起钩来( Domenico， 1977; Harvey，1993; Wang，2002; Dutta et al. ，2009; 郝艳军等，2016) . 利用一些简明的理论关系式或经验关系式，将阻抗与储层物性参数建立起联系，就能进一步计算出储层物性参数了，这是储层物性间接反演的思路. 也可以从波动理论出发，建立复杂的数学物理模型，利用专业的数学算法求解波动方程来得到各项储层物性参数，这是储层物性波动方程反演的思路. 另外，地质统计反演在储层物性的空间展布预测方面可以发挥独特的优势，这与传统反演关注垂向预测的重点有所不同( Haas and Dubrule，1994) . 近年来，人工智能技术也被用于储层物性的预测当中，其优点是打开了多学科数据融合的大门，通过数据驱动的学习可以在数据和预测目标值之间建立起高度非线性的关系( Schultz et al. ，1994a， 1994b; Ronen et al. ，1994) . 同时，也可以利用统计岩石物理分析方法来得到储层物性参数，这是一种处理复杂岩性和储层非均质 性 的 手 段，非常适合复杂多变的陆相沉积环境 ( Avseth et al. ，2001) .

　　下面依次论述阻抗反演技术、储层物性预测技术和岩石物理分析技术.

　　1 阻抗反演技术阻抗反演技术

　　实现了从地震振幅到地层阻抗的转换. 声阻抗是地层的一种物理性质，被定义为地层密度 ρ 和地层中地震纵波速度 Vp 的乘积，即 ρVp . 声阻抗反演诞生于 1979 年 ( Lindseth，1979) ，弹性阻抗反演诞生于 1999 年( Connolly， 1999) . 阻抗反演最大的好处是能够将反射界面的性质转换成地层的性质，这为储层物性参数的预测与评估奠定了资料基础.

　　在阻抗反演过程中，地震数据的频带宽度非常重要，尤其是低频信息要足够丰富( Pedersen-Tatalovic et al. ，2008) .实际上，地震数据的频带宽度一般为[5，50]Hz，缺失高频则对薄层的分辨能力降低，缺失低频则无法得到绝对阻抗值 ( 如图 2 所示) . 图 2 强调了低频对反演结果的重要性. 对一个简单的层状介质模型( 黑色) 来说，缺失低频信息的话，无论高频成分如何丰富( 相对于( a) 、( b) 中的高频成分大为增加，因而对薄层的分辨能力得到了提升) ，都不能得到绝对阻抗值( 只有( c) 得到了绝对声阻抗) . 所以，利用测井数据或地质信息来扩展地震数据的频带宽度是一项非常关键的工作，这同时也是地震采集和处理所要努力达到的目标.

　　在图 3a 中，对测井得到的声阻抗曲线分别进行上限为 60 Hz 和 8 Hz 的高阻滤波，可以看到声阻抗曲线的变化，下部是对应的频率谱的变化; 图 3b 展示了一个典型的地震道及其频带宽度，低频和高频成分都是缺失的. 此例进一步表明，单纯依靠地震频带的宽度进行反演，既不能保证反演分辨率的提高，也不能保证阻抗绝对值的获得.

　　生产中应用最广泛的三参数同时 AVO 反演是以方程式 ( 1) 为基础的，同时利用了最常用的基于地质模型的反演技术，反演结果示例见图 4. 图中也给出了反演结果( ( a) 声阻抗和( b) 纵横波速度比) 与测井中得到的值的对比曲线，二者一致性良好.

　　弹性阻抗反演结果的示例见图 5. 伽马和电阻率测井曲线指示出了含烃地层，与此相反，EI( 0°) 曲线( 即声阻抗曲线) 对此并没有响应，而 EI( 40°) 却有明显的响应变化. 此例中，弹性阻抗突出了Ⅱ类 AVO 响应的指示特征.

　　阻抗反演是目前应用最广泛的一种地震反演预测技术，但是阻抗并不是一种直接的储层物性参数，仍然不是地质学范畴内的术语，只是地层密度和速度的乘积，地质学家和地球物理学家更希望得到直接表征储层物性的参数，因此，还需要进行进一步的工作，求取各项储层物性参数.

　　2 储层物性预测技术

　　2. 1 间接反演

　　间接反演技术实现了从阻抗到储层物性参数的转换，包括岩性识别参数、孔隙度、油气饱和度、渗透率、杨氏模量和脆性指 数 等 弹 性 力 学 参 数 等 ( Smith and Gidlow，1987; Smith，2010) .

　　间接反演具有简单易操作的优点，目前在实践领域得到了广泛的应用，不过，反演过程中很关键的一步是需要用到媒介关系，来将储层物性参数与阻抗联系起来. 这种媒介关系一般是根据简单的理论关系或是经验认识得来的，对其普适性和有效性都需要保持警惕.

　　2. 2 波动方程反演

　　如果想要利用地震数据进行储层物性的直接反演，就需要理解背后的波动机理，以便将地震观测结果与储层物性挂起钩来，即通过地震速度、振幅和衰减等信息来直接反演储层固体及所含流体的物理性质( Fjaer et al. ，2008) .

　　根据对岩石样品的微观静态观测结果和动态观测结果，人们对岩石固体骨架及所含流体的动力学机制有了更加深入的了解，可以由此总结提炼出主控物理机制，以理解地震波作用下的储层岩石响应，如图 8 所示.

　　当然，我们还可以更进一步考虑更加复杂的机制，所带来的结果就是波动方程的进一步复杂化和求解过程的更加困难，这方面的内容可参阅 Yang 和 Zhang( 2000)

　　.在波动理论研究方面，固液两相介质波动理论已经发表出来了半个多世纪，这期间又涌现出了各种波动理论，对岩石孔隙结构及其中的流体做各种不同的模型简化处理. 这些波动理论的基石是 Biot 理论( Biot，1956a，1956b，1962) ， Biot 从宏观尺度研究了流体流动的效应( 参考式( 12) ) . 后来发展出的 BISQ 理论和斑块饱和模型理论分别引入了微观尺度和中观尺度下的流体流动效应( 孙卫涛等，2015; Zhang et al. ，2019) . 比如以部分饱和孔隙介质 BISQ 模型为基础，利用杂交遗传算法求解这个模型，能够直接反演出储层的孔隙度、油气饱和度和渗透率等参数( Nie et al. ，2004; Fang and Yang，2015) . 这种直接反演结果是基于复杂的理论模型假设的，求解过程也是基于专业数学算法的，对石油工业界的从业人员来说，在模型的理解和反演求解操作方面都会遇到不小的障碍，因此，这种专业的直接反演工作主要还是由世界 上 的 各 大 高 校 来 推 动 的 ( Batzle and Wang，1992; Berryman and Wang，2000; 印兴耀等，2015) .

　　理论和实验一直都关注速度和衰减的频散效应，如图 9 ( White，1975; Harris et al. ，1997; Sams et al. ，1997; King and Marsden，2002; Pride et al. ，2003) . 地震频段的岩石物理实验分析是了解波动机理不可或缺的手段，近年来也得到了长足的发展( Yin et al. ，2017) . 举例来说，图 9a 给出了 Foxhills 砂岩样品的纵波速度和横波速度的变化情况，测试时荷载频率和环境温度是变化的，岩样有干燥和甘油饱和之分( Batzle et al. ，2006) . 此类实验给出了孔隙流体的流动给波速带来的改变( 示意图见图 9b) ，能够据此推测流体的流动机制及波动机理，既可以验证理论预测的正确性，又可以 指导理论模型的建立 ( Dvorkin and Nur，1993; Dvorkin et al. ，1995) .

　　关于地震反演的算法，这里举两个有代表性的例子. 一个是早期的三参数同时反演过程中的数学算法，一个是求解 BISQ 模型参数过程中的数学算法. 对于三参数同时反演算法来说，这是一个同时求解出 ρVp、ρVs 和 ρ 的过程( 方程式 ( 1) ) . 根据地震响应的褶积模型理论，可以将求解公式写成矩阵求逆的数学过程. 不过，如果直接进行求逆的话会有两个问题，一个是这一过程非常耗时且不稳定，另外一个就是求逆过程中无法加入低频成分. 较为稳定的解决办法就是给出一个 初 始 地 质 模 型，通过共轭梯度法进行迭代计算 ( Hampson，1991; Russell et al. ，2006) . 各大商业软件一般是基于此类思想进行反演计算的. 但是，对 BISQ 这种模型来说，公式极其复杂且参数较多，想要进行反演求解的话，需要更加专业的数学算法，包括遗传算法类的人工智能算法. 具体的 数 学 算 法，读 者 可 参 阅 杨 文 采 ( 1992 ) 、Russell 等 ( 2006) 、刘福平等( 2010) 、Fang 和 Yang ( 2015) 、孙成禹等 ( 2019) 和 Zhang 等( 2019) 的论文. 求解结果 示 例 见 图 10 ( Fang and Yang，2015) .

　　2. 3 地质统计反演与人工智能预测

　　在石油工业界，地质统计方法的应用起始于用 kriging 技术来绘制地质图以及岩石物理参数的展布图 ( Krige， 1951; Matheron，1963; Haas and Viallix，1976; Haas and Dubrule，1994) . 关于地质统计反演在石油勘探开发领域的 历史及现状，可参考 Chambers 等( 2000a，2000b) 、Trappe 和 Hellmich( 1998，2000) 、Francis( 2006a，2006b) 以及赵鹏飞等 ( 2019) .

　　随机地质统计方法与 kriging 方法不同，现在随机反演之所以得到重视，就是因为它能够给出储层的非均质性特征，这在模拟油藏的流动模式时是非常有用的( 沈洪涛等， 2017; 王小丹等，2018) . 此外，随机反演可以额外引入地震信息和其他有用的信息，这也是这种方法受欢迎的一大原因.随机反演使用地质、测井和岩心统计的岩石物理参数统计分布图和三维变差场，在参数的统计分布范围内通过随机采样得到一个值来进行正演，将正演结果与实际地震特征比对，符合地震特征的就可以作为一个可能的结果. 与 kriging 方法只提供一个最佳结果不同，随机反演可以提供无数个可能的结果，每一个都符合井特征和地震特征. 将许多个随机反演结果进行平均，其结果将会与 kriging 方法得到的结果接近. 图 12 给出了 4 个随机反演的阻抗分布结果，彼此间的差异明显，通过正演得到合成地震记录，每一个都可以很好地匹配实际地震记录( Francis，2006b; Simm and Bacon，2014) .关于随机反演的数学算法，Chambers 等( 2000b) 列举了 6 种主要的随机反演数学算法，其中最容易理解的要数序列高斯模拟算法( Haas and Dubrule，1994) ，这种算法的思路比较直接但计算效率低，其他算法的目的在于提高计算效率.

　　Kriging 方法以及 Cokriging 方法与前面提到的阻抗反演方法和间接反演方法都属于确定性反演方法. 常规阻抗类反演受地震频带宽度的限制，适用于较厚的地层且横向变化不大，因此这种确定性方法只能提供一个比较粗略和平均化的结果. 在储层物性已知的分布范围内，随机反演可以提供无数个可能的结果，逼近真实的存在情况. Francis( 2006a) 曾经举例说明了确定性反演和随机反演的区别，比如一个班级内学生身高的情况，确定性方法只给出平均身高信息，而随机方法可以给出每一个学生的身高信息以及彼此之间的差异 ( 平均之后将等于确定性方法的结果) .

　　近 20 多年来，地质统计方法在油田开发领域得到了广泛应用，但受勘探地球物理学家接纳的普遍程度并不高，主要是因为这背后有太多的数学处理过程，而直观的地质意义和物理意义又不那么透明，另外，与油藏模拟主要依赖井信息不同，勘探阶段的地质统计方法要靠地震信息，而阻抗反演和储层物性间接反演在应用领域已经占据了统治性地位，地质统计方法在勘探领域仍属于新兴者. 关于地质统计反演的具体内容，读者可参阅 Simm 和 Bacon( 2014) .

　　近年来，人工智能( AI) 在油气勘探开发领域成为了热点. 在储层物性预测方面，人工智能也被给予了厚望( Schultz et al. ，1994a，1994b; Trappe and Hellmich，1998; Hall， 2016; 余为维等，2016; 林年添等，2018; Russell，2019; Shaw et al. ，2019) .

　　人工智能算法的作用在于，通过学习大量的数据信息来总结储层物性参数和数据特征之间的关系，这是一种数据驱动的预测方法. 例如，我们已经知道了孔隙度和阻抗的关系，并可以借用物理机理来进行合理地解释，但是大多数情况下，由于地质情况的复杂性，我们很难得出新的确定性的物理关系，即使使用地质统计方法，也要符合统计学的基本原理才行. 人工智能打破了这种限制，可以在数据信息中通过学习总结出储层物性和数据之间的非线性关系. 与其他的物理推导和地质统计方法不同，其最大的好处是提供了一种信息融合的途径，可以同时利用地质、地震、测井、岩心和其他一切有用的信息.

　　以人工神经网络( ANN) 为例( Ronen et al. ，1994) ，如果我们有一些( x，y) 类型的数据( ( 2. 1，5. 0) 、( 0. 6，1. 8) 、 ( 9. 4，2. 02) 、( 6. 7，13. 9) ) ，想要预测 x = 4. 0 时的 y 值. 在传统方法中，通过直线拟合可得 y = 2. 06x + 0. 54 的形式，从而 y( 4. 0) = 2. 06 × 4. 0 + 0. 54 = 8. 78. 如果用 ANN 来进行预测，如图 13a 所示，利用前面的 4 组数据对进行训练( 学习) ，结果得到 ANN 的基函数 f1 ( x) = x 0 ，f2 ( x) = x 1 ，以及权值 w1 = 0. 54，w2 = 2. 06. 这样就训练好了一个 ANN，在输入层输入 x 的值( 4. 0) 就可以用这个 ANN 来进行预测了. 如果有三个输入数据( 比如 x1 = 阻抗、x2 = 地震瞬时频率、x3 = 深度) ，要预测的是孔隙度( y( x) ) ，ANN 的形式如图 13b，这里只有一个隐含层，此例中需要通过数据训练得到 5 个基函数，因此需要至少 5 口井的信息和井周围的地震信息.

　　图 14 是利用人工智能预测的结果示例( Schultz et al. ， 1994b; Hall，2016) . 在图 14a 的例子中，有一些井资料，在每口井中都进行了 5 种类型的测井，从每口井取出的岩心中划分出了对应的 9 种岩性，剔除一口井以作后续的验证用，将其余的井数据来训练支持向量机( SVM，一种有监督的机器学习算法) . 之后用训练好的 SVM 和验证井的测井数据来预测这口井中的岩性划分，并与这口井中已知的岩心信息进行对比. 经过计算，此例中用 SVM 进行岩性预测的正确率为 43%，抛开相似岩性的干扰，正确率为 88% . 在另外一个例子中，训练出了一个可以通过测井数据和地震数据预测孔隙度的 ANN，通过这个 ANN 来进行三维孔隙度的预测，结果如图 14b.

　　与其他反演方法的应用目的不同，地质统计方法和人工智能方法的应用目的在于预测储层物性的空间展布特征，二者之间的比较参见 Trappe 和 Hellmich ( 2000) . 人工智能打破了学科领域界限，能够以一种非明确的方式在地震数据和储层物性之间建立起一种关系，但是地质学家和应用地球物理学家对人工智能算法的熟悉程度往往并不高，更多的是将其当作黑箱来处理，这种不透明性可能是其发展的最大障碍. 另外需要注意，在学习和训练模型的时候，与传统方法一样，专业领域知识的作用一点也不可以被弱化.——论文作者：韩宏伟，程远锋* ，张云银，王兴谋，曲志鹏，隋志强，冯德永，梁鸿贤，王玉梅，慎国强