b值的时空分布特征与地震危险性的关联分析

发布时间：2022-01-21

　　0 引 言

　　在统计地震学研究中，古登堡-里克特提出的震级-频度关系 lgN = a - bM 是 最 基 础 的 规 律 之 一 ( Gutenberg and Richter，1944) . 震级-频度关系中的 b 值表征了不同震级地震频数所占的比例，但它不仅仅是一个统计分析参数，还具有直接的物理意义( 李全林，1982) . 虽然，不同研究者对 b 值的物理背景有着不同的理解( Mogi，1962; Scholz，1968a; 李纪汉，1987; Wiemer et al. ，1997，1998; Schorlemmer et al. ， 2005) ，但普遍认为 b 值与应力变化以及与介质不均匀性有关. b 值的统计计算方法主要采用最小二乘法和极大似然法 ( 张建中和宋良玉，1981; 吴果等，2019) . 研究表明，b 值的时间变化特征可以用来预测未来大地震发生，空间变化特征可以用来判别强震危险性区 ( 易桂喜等，2004，2005，2006， 2007，2008; 刘静伟等，2010; 李正芳和周本刚，2014) .

　　本文首先回顾了地震活动性参数 b 值的定义和物理背景，分析了 b 值的计算方法以及影响因素. 对 b 值随时间变化的类型进行了总结归纳，将 b 值随时间变化的特征归纳为以下 4 类: ( 1) 在大震发生前的几年时间，b 值升高，主震发生后，b 值下降; ( 2) 在大震发生前几年，b 值降低，主震发生后，b 值升高; ( 3) 大震发生前 b 值会明显下降，并在回升过程中发生大震; ( 4) 在大震发生前，b 值升高，但在主震前短时间内有前兆下降. 指出大震前的低 b 值特征是强震前的异常现象，认为地震前 b 值的时间变化是地震预测的重要前兆，并进一步探讨了 b 值随时间变化应用于地震预测中的可能性. b 值的空间变化反映了强震区应力集中和转移，并按照构造特征对 b 值空间变化特征进行分类: ( 1) 正断层的 b 值最高，走滑型断层次之，逆断层的 b 值最低; ( 2) 沿着不同断层段 b 值的变化: 在断层的蠕滑段 b 值较高，在凹凸体段 b 值较低; ( 3) b 值随着深度的变化: 在浅深度处 b 值较高，在较深的地壳深度处 b 值较低. 指出异常低 b 值区指示高应力积累，能够判识强震危险性区. 最后，对利用数值模拟建立人工地震目录研究 b 值、利用小震资料获得区域精细 b 值空间分布、以及在地震危险性中的应用等问题进行了讨论.

　　1 b 值

　　1. 1 b 值的定义和物理背景

　　Gutenberg 和 Richter( 1944) 提出的震级-频度关系 lgN ( M) = a - bM 是地震活动性参数研究中的最基础的规律. 这是一个经验公式，式中 M 是地震震级，N 代表在一定时间内大于或等于震级 M 的地震数量，截距 a 取决于研究区和时间窗的范围，Rundle( 1989) 认为 a 值代表研究区的地震活动总体水平，斜率 b 代表大震和小震的比例关系，低 b 值代表大地震在所有地震中所占比例较大，高 b 值则代表小地震在所有地震中所占比例较大.

　　有关 b 值物理背景的研究有多种认识，包括地应力、震源深度、介质的各向异性、地热梯度等. Mogi( 1962) 和 Scholz ( 1968a) 根据岩石模拟试验的研究结果，分别提出了对 b 值随时间与空间变化的机理认识. Mogi( 1962) 以为介质的不均匀性，是导致 b 值变化的主要因素，b 值越大，介质的不均匀性就越显著; Scholz( 1968a) 则依据单轴与三轴岩石压力实验结果，提出了岩石所处的应力状态决定了 b 值与它的变化，即 b 值 越 低，就 表 明 应 力 越 高. 此 外，Warren 和 Latham ( 1970) 提出了热流梯度与 b 值有关的观点，认为 b 值也会随着热流梯度增加而增加; Wyss( 1973) 提出有效应力的增加使 b 值降低; 李纪汉( 1987) 验证了 Mogi 和 Scholz 的结论，认为应力与介质不均匀性是 b 值的重要影响因素; Wiemer 等 ( 1997，1998 ) 指出 b 值受应力和介质非均匀性 的 影 响; Urbancic 等( 1992) 利用岩爆后的低震级事件确定了 b 值与应力释放的时空相关性; Schorlemmer 等( 2005) 的岩石实验结果进一步表明，b 值与剪应力大小成反比，低 b 值具备更高的应力积聚; El-Isa 和 Eaton( 2014) 认为 b 值与构造应力有很大关系.

　　基于 b 值和应力状态之间的关系，国内外许多学者利用 b 值研究了地震活动、地震构造特征. 易桂喜等( 2004) 利用 b 值水平与构造应力水平成反比，勾绘了安宁河—则木河断裂带的凹凸体; 易桂喜等( 2006) 利用了 b 值与应力的反比关系判定了龙门山—岷山断裂带的现今活动习性与强震危险性; Nanjo 和 Yoshida( 2018) 认为 b 值与差应力成反比，并据此判定了日本南海海槽地震的初始破裂部位; 谢卓娟等( 2019) 利用低 b 值与高应力积累的对应关系研究了京津冀地区的地震活动性.

　　在实验室以及实际地壳观测中，b 值与差应力的反比关系已经得到了广泛承认与使用. 由此而论，b 值作为应力的一个表征值，可以帮助标识未来可能发生破裂板块边界上凹凸体或高应力段( Nanjo et al. ，2020) . 活动断裂带上具备高应力积累的凹凸体或闭锁断裂段容易发生强震( Aki，1984; Wiemer and Wyss，1997; Wyss et al. ，2000) . 根据 b 值与应力的反比关系，运用 b 值空间分布特征的差异性，可以得到不同断裂带应力积累程度的差异，进而分析地震危险性.

　　1. 2 b 值的计算方法与影响因素

　　当前 b 值的计算方法主要有线性最小二乘法、非线性最小二乘法、极大似然法和矩估计法，其中矩估计法可以视为极大似然法的一种( 张建中和宋良玉，1981) . 最常见的 b 值的计算方法是线性最小二乘法和极大似然法.

　　大量的研究表明，最小二乘法简便易行，是拟合 b 值常用的办法( 李全林等，1978; 黄玮琼等，1989; 易桂喜等，2004， 2005，2006; 刘 静 伟 等，2010; 谢 卓 娟 等，2019 ) . 但 Felzer ( 2007) 认为最小二乘法可能受到大、小震级的地震所占权重不同的影响，而最大似然法对每一次地震的权重相等. 近年来极大似然法拟合 b 值的方法已经逐步发展起来( Aki， 1965; Utsu，1965; Wiemer and Wyss，2002; 龙锋等，2009; 李正芳和周本刚，2014; 谢卓娟等，2015; 刘静伟和吕悦军，2016; 吴果等，2019) .

　　原则上，采用最小二乘法拟合 b 值应该与极大似然法拟合的结果相似，但实际上，对于相同的地震数据，这两种方法不一定产生相同的 b 值. El-Isa( 2013) 指出在某些情况下，使用不同的计算方法所引起的 b 值差异可能与不同的时间和空间所引起的差异一样大. 因此，用不同的方法拟合 b 值，可能会引起 b 值在时间和空间上的差异. 张建中和宋良玉 ( 1981) 经过蒙特卡洛模拟，得出了极大似然法的计算误差、计算量以及计算所需的样本量都小于线性最小二乘法的结论. 李世杰等( 2018) 利用拟合地震目录和天然地震目录，也得到了类似的结论，并进一步探讨，认为随着样本量的增加，两种方法计算结果的差别越来越小. 目前，国外已经极少使用最小二乘法.

　　影响 b 值计算结果的要素有很多，包括地震目录的完整性、余震的删除、起始震级的确定和震级间隔的选取，以及样本量的大小等( 黄玮琼等，1989; 任雪梅，2011) .

　　( 1) 地震目录的完整性

　　理论上，根据 G-R 关系式得到的震级-频度关系是线性的，但是实际资料显示两者之间并不是线性关系，尤其是在小震级段和大震级段会出现偏离线性的现象. 在小震级段有 “掉头”现象; 在大震级段则存在“摆尾”现象. Wiemer 和 Wyss( 2000) 认为“掉头”现象是由地震目录的不完整造成的. 完整可靠的地震资料是统计 b 值的根据，因此，分析资料的完整性和可靠性十分必要.

　　历史地震是按照历史资料记录分析得到的，一般来说，年代越早，地震漏记的可能性越大( 黄玮琼等，1994) .

　　由于监测仪器、监测环境等种种原因，地震台网监测能力是有限的，一些小震和微震时常被漏记，因此也有必要对现代地震目录的完整性进行研究. Wiemer 和 Wyss( 2000) 认为现代地震数据的质量可以用区域最小完整震级 MC 表示，拟合效果测试法是估计最小完整性震级的多见手法，这种方法的优点是操作简单、计算便捷迅速，它的根本原理是依照 G-R 关系的幂率分布来拟合切实的震级-频度分布.

　　( 2) 删除余震

　　一般认为，余震活动的丛集特征在某些程度上掩盖了地震作为独立事件的统计特征，使地震活动的时空分布偏离了正常活动状态. 陈凌等( 1998) 在研究中指出，在地震活动性分析中，删除余震的目的是消除地震之间的相关因素，使地震的产生尽量满足平稳性、互相无关性，即满足泊松模型. 因此，在估计 b 值之前，要先用合理的方法删除余震. 常用的删除余震的方法有 G-C 法、C-S 法、K-K 法等( 陈凌等，1998) .

　　( 3) 起始震级和震级间隔

　　采用不同的起始震级和震级间隔来计算 b 值，计算结果存在较大差别，因此，有必要根据具体情况，选择合适的震级范围. 在统计中，多将最小完整震级 Mmin作为统计的起始震级. 黄玮琼等( 1989) 在研究中提出的看法是，对于历史地震来说，起始震级 Mmin取 5. 0，震级间隔 ΔM 取 0. 5 较为合适.但有些学者有不同的观点，潘华和李金臣( 2006) 认为在地震样本量 N 满足要求的前提下，尽量提高起始震级.

　　( 4) 样本量 N

　　由于震级-频度关系是统计公式，而样本量 N 不足会严重影响震级-频度公式的线性关系，因此样本量 N 对 b 值的计算有十分重要的影响. 张建中和宋良玉( 1981) 和李世杰等( 2018) 都利用蒙特卡洛模拟的方法就样本量对 b 值的影响进行了讨论，并都得出了极大似然法对样本量的需求小于最小二乘法的结论; 任雪梅( 2011) 也得出了相同的结论，并指出产生这种现象的主要原因是最小二乘法使用线性的震级-频度关系拟合 b 值，而样本量不足会影响震级-频度关系的线性关系.

　　2 b 值的时间分布特征与地震活动性

　　2. 1 b 值随时间变化特征

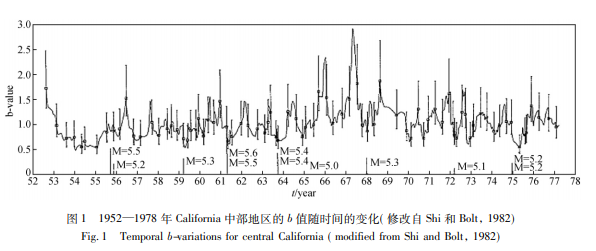
　　地震活动在时间上是不均匀分布的. 尽管 b 值随时间的变化有很好的记录，但观测结果却是各不相同的，在大地震之前，有些地震的 b 值是前兆减小，还有些地震的 b 值是前兆增加. 图 1 是 1952 年到 1978 年加州中部地区的 b 值随时间变化的图像，通过该 b 值图像可知 b 值涵盖了从 0. 5 到 2. 5 以上广泛的范围( Shi and Bolt，1982) . 图 2 是强震前 b 值随时间变化的一般模式( Wang，2016) . 在发生地震之后的很长一段时间内，b 值处于平均值附近. 在时间 t1 处，b 值从正常值增加到 t2 处的峰值，然后在时间 t3 处下降到正常值.当 t > t3 时，b 值在正常值附近变化或随时间减少，直到 t4 时刻，主震发生. 大震发生之前，出现的 b 值异常时间被称为前兆时间. 图 2 中的 T 和 T'分别表示两种常见的前兆时间，其中 T 是指 b 值从正常值开始异常增加的时间点至主震即将发生的时间点之间的时间段，即 T = t4 - t1 ; T'表示的是 b 值异常达到峰值的时刻至主震即将发生的时刻之间的时间段，即 T' = t4 - t2 . 另外，主震发生前的等待时间 T* 指的是 b 值恢复到正常值的时刻至开始降低到主震即将发生的时刻之间的时间段，即 T* = t4 - t3 .

　　b 值随时间变化的观测结果是各不相同的，在大地震发生之前，有些地震的 b 值减小，还有些地震的前兆是 b 值增加. 关于大震前 b 值随时间的变化可归纳为以下 4 类:

　　( 1) 在大地震发生之前的几年时间，b 值升高，主震发生之后，b 值下降，Fiedler( 1974) 和 Smith( 1981) 在委内瑞拉， Smith( 1981，1986) 在新西兰和加利福尼亚的研究都支持这种观点;

　　( 2) 在大地震发生之前几年，b 值降低，主震发生之后，b 值升高( Scholz，1968b; Wyss and Lee，1973; Urbancic et al. ， 1992; Wiemer and Wyss，1997; Wiemer et al. ，1998; Wyss et al. ，2004; Wyss and Stefansson，2006) ;

　　( 3) 李全林等( 1978) 指出在大震发生前 b 值会明显下降，并在回升过程中发生大震，比如: 1976 年唐山地震，1971 年下半年 b 值开始上升，1973 年下半年开始下降，1976 年初回升，回升过程中发生了 7. 8 级地震( 图 3) ;

　　( 4) 在大地震发生前，b 值升高，但在主震前短时间内有下降的前兆，Sahu 和 Saikia( 1994) 发现，1988 年 8 月印度— 缅甸地震，b 值由 1976 年的 0. 6 逐渐上升到最大值 1. 33，但 1987 年 7 月份 b 值在地震发生前出现短期下降.

　　2. 2 b 值与地震预测

　　地震前 b 值的时间变化被认为是地震预测的重要前兆. Smith( 1981) 等人的研究表明对于一些特定的地震序列，b 值会在主震前后发生变化，相较于余震，前震序列的 b 值更小.这一特性与初始的高应力状态随着主震而降低相一致，因此， b 值随时间的变化被认为有助于地震预测( 李全林等，1978) .

　　不管大地震是否有前震，主震之前若干年内的地震活动是有异常的. 大震前的低 b 值特性，屡次得到震例检验: 李全 林等( 1978) 在研究中指出在大地震发生前 b 值会明显下降，在回升的过程中发生大震，支持这种观点的震例包括 1975 年辽宁海城地震、1976 年唐山 MS 7. 8 地震等; 马鸿庆( 1978) 研究了华北地区九次大震周围区域的 b 值，也发现震中较小范围内的 b 值随时间先升高再逐渐降低到最小值，在地震之前有所回升，然后地震发生. Nanjo 等( 2012) 的研究表明 2004 年印尼 9. 1 级地震和 2011 年日本 9. 0 级地震发生之前，都有明显的 b 值降低. 王辉等( 2012) 对川滇地区 1980 年以来 M 6. 5 的地震资料分析表明，震源区震前的 b 值出现整体下降的走向，58% 的震源区的 b 值在强震前有明显的下降走向. 史海霞等( 2018) 探讨了汶川地震前的 b 值变化，研究表明从 2000 年开始到汶川地震前的 b 值长期趋于减小，在汶川地震约半年前呈现迅速、明显的下降.

　　因此，地震活动性参数 b 值在地震预测中的应用表明，地震前的低 b 值特征可以作为地震活动异常现象的判断依据. 另外，b 值的空间分布可以用来准确预测破裂区域.

　　3 b 值空间分布特征与地震活动性

　　3. 1 b 值空间扫描

　　地震活动参数 b 值在空间上的分布特征也是非均匀性的. b 值在空间上的分布特征可以归纳如下: ( 1) b 值随区域构造特征和主要断层类型的变化，正断层的 b 值最高( b > 1) ，走滑型断层次之( b ～ 1) ，逆断层的 b 值最低( b < 1) ( Schorlemmer et al. ，2004; 刘静伟等，2016) ; ( 2) 沿着不同断层段 b 值的变化，在断层的蠕滑段 b 值较高，在凹凸体段 b 值较低( 易桂喜等，2008，2010; 李正芳和周本刚，2014) ; ( 3) b 值随着深度的变化，在几千米的浅深度处 b 值较高，在较深的地壳深度处 b 值较低( Wiemer et al. ，1996，1998) .

　　对 b 值空间扫描的研究由来已久，李全林等( 1978) 认为对 b 值变化进行动态的时空扫描是观测应力集中和转移，监视破坏性地震孕育的一种方法. 黄德瑜和冯浩( 1981) 利用 b 值空间扫描方法在大范围内搜寻，辨别孕震的危险区. Wiemer 和 Wyss( 1997) 提出精细 b 值空间扫描，用异常低 b 值区对应高应力凹凸体，异常高 b 值区对应蠕滑断裂段的方法，并应用在强震危险性研究中. 已有研究( 易桂喜等，2004; Wiemer and Wyss，2002; 刘静伟等，2016) 中采用的 b 值空间扫描方法为: 首先将研究区划分为等间距的网格，然后根据以每个网格节点为圆心、r 为半径的圆形统计单元内的地震资料，选取合适的拟合方法计算地震活动性参数 b 值，并以此作为单元中心点( 即网格节点) 的地震活动性参数，并绘制其空间分布等值线图.

　　易桂喜等( 2004，2005，2006，2008，2010，2013) 将 b 值的空间分布特征先后应用于安宁河—则木河断裂带、鲜水河断裂带、龙门山—岷山断裂带、川滇地块东边界、川南马边地区以及龙门山断裂带南段等地区的地震危险性分析. 因此，地震活动性参数 b 值在地震危险性研究中的应用表明，b 值的空间扫描结果可以成为判断未来强震危险性的一个指标.

　　3. 2 b 值与地震危险性

　　区异常低 b 值区指示高应力累积，能够进一步指示强震危险性区. 活动断裂带上具有高应力积累的凹凸体或闭锁断裂段是强震的易发地( Aki，1984; Wiemer and Wyss，1997; Wyss et al. ，2000) . 大量研究表明，应力与 b 值是反比关系，b 值越低，应力水平越高. 利用 b 值空间分布特征的差异性，可以反映出不同断裂带的应力积累水平的差异，进而反映地震危险性的空间差异性. 易桂喜等( 2004、2005、2006) 将 b 值的空间分布与多地震活动性参数值组合，用在判识断裂带各段落的现今活动习性与强震危险性. 李莹甄等( 2005) 用相同的方法判定了天山各分区的地震活动性; Schorlemmer 和 Wiemer ( 2005) 发现 b 值的空间分布可以用来准确预测破裂区域，尽管地震的时间仍然是不可预测的; 王玉婷等( 2012) 使用多地震参数组合法并结合 b 值的空间分布图像展现和推测了河北平原地震带活动断裂带各段落现今应力积累的相对水平.

　　除了多地震活动性参数组合法，还可以结合历史和现今地震活动背景，剖析和判断研究区主要断裂带的现今活动习性，以及相对应力水平的空间分布特征，并与板块运动特征、地质构造特征等相结合，进而归纳判断现今处于相对高应力状态的潜在强震危险区，并为强震预测提供地点信息; 如果该区域有足够多的历史地震资料，还可以合理地估计出各断裂段的强震复发周期，结合强震的复发周期，为强震预测提供时间信息. 易桂喜等( 2008) 讨论了川滇块体东边界断裂带的应力空间分布与强震危险性，并据此指出了多个凹凸体以及川滇块体东边界将来大震或强震的震源区( 图 4) . 王辉等( 2011) 利用华北地区 1970—2009 年的小震资料，给出了 b 值空间分布和强震复发间隔等的空间分布，结合板块运动特征、构造地质资料以及动力学资料，剖析了华北地区的背景地震活动，研究结果反映了华北地区背景地壳应力水平，也为区域未来地震危险性提供了判别依据. Nanjo 和 Yoshida ( 2018) 指出日本南海海槽的 b 值与差应力、滑动亏损速率的反比关系，而且，东部高滑动亏损速率区域的 b 值低于西部地区，这说明东部凹凸体上的差应力高于西部地区. 这可以解释南海海槽地震记录中，往往是东部首先破裂( 图 5) .

　　4 讨 论

　　4. 1 存在的问题

　　b 值计算结果的可靠性主要依赖于地震资料的完整性和精度，而历史地震资料不完整，现代地震资料年限较短，而且空间分布不均匀. 进一步改善地震资料的精度和完整性，是 b 值研究的关键.

　　对于 b 值计算方法的选取，仍存在争议. 对同一区域的地震目录使用不同方法拟合 b 值得出的结果可能会有差异; 另外，由于对 b 值拟合结果的影响因素众多，尽管使用的是同一种计算方法，因为起始震级 Mmin，样本量 N 以及震级间隔 ΔM 等参数的不同，所获取的结果也可能存在差异. 因此，根据不同的影响因素选取适当的计算方法也十分重要.

　　目前，起始震级的选取方法众多，并且起始震级的选取标准并不一致. 大多数学者认为起始震级应该选取最小完整性震级 MC ; 但是少数学者却认为在地震样本量 N 足够大的情况下，应该尽可能大的提高起始震级( 潘华和李金臣， 2006) . 由于起始震级的选取对 b 值的计算结果会有影响，所以需要验证这两种方法的优劣性，选取合适的起始震级进行计算.

　　在地震预测中，b 值异常作为地震的前兆是多样性的.根据震例总结，发现 b 值降低或升高都可能发生地震，无异常有可能发生地震，有异常也可能不发生地震. 对 b 值异常现象缺乏独特的物理解释，这可能仍然是一个问题. b 值的影响因素众多且复杂，包括地应力、介质的各向异性、地热梯度等，仍需进一步探讨. 如果 b 值的变化不是地应力的变化所引起的，那么是否有可能受到其他影响因素变化，从而引起 b 值变化. 所以，如何根据 b 值异常进行地震预测是一个比较值得思考的问题.

　　4. 2 未来的研究方向

　　b 值的计算关键依附于记录完全的地震目录. 但是提高观测资料的样本量和精度，不是一蹴而就的，人工地震目录模拟可以改善目前已有地震目录不完整性、填补大地震资料稀少等问题. 因而，利用数值模拟方法建立人工地震目录，是地震活动性 b 值研究的一个方法. 人工地震目录模拟的方法有很多，在未来的研究工作中，可以考虑多种模拟方法相结合，以求模拟出的地震目录能够达到更好的效果.

　　随着全国地震台站数目的不断增长和地震台网监测能力的不断进步，地震目录的数量和精度都在迅速提高，能够更好地进行 b 值研究工作. 在未来的工作中，对区域精细 b 值空间扫描的研究将会增加，地震数据质量的提高也能更好地服务于地震预测以及判定地震危险性区等研究工作.

　　在地震危险区判识方面. 由于大震的发生频度小，大震的地震目录数量少，因此可以利用大量的小震数据识别凹凸体，但是小震数据源自身获取的不确定性会对 b 值空间分布产生直接影响，因此，为了减小这种不确定性，很多科研人员在使用小震数据前会先进行小震精定位. 未来研究工作中可以结合小震精定位技术，利用重定位之后的数据结果，绘制出 b 值空间分布图，结合地震地质资料，更加精确地判识出地震危险性区.

　　在地震危险性评价方面. 通过对某些地区的活动性统计分析，获取与地震危险性评价相关的 b 值、地震年发生率 ν 等活动性参数，对相关地区的地震危险性进行评价. 估计出可靠的、具有长期代表性的震级-频度关系参数 a 值和 b 值，接着由地震年发生率公式 ν( M) = 10( a - bM) 估算出震级 M 以上的年发生率，最后利用地震的 a 值、b 值和年发生率 ν 值估算出破坏性地震的发生概率.

　　5 结 论

　　本文综述了地震活动性参数 b 值的研究，包括 b 值的内在性质和理论，b 值随时间的变化和 b 值的空间分布. 地震活动性参数 b 值不只是一个简单的分析统计参数，它还具备直接的物理意义. 经过研究人员几十年的探索，不同的研究者对地震 b 值的物理背景有着不同的理解，包括与应力状态的反比关系以及与介质的各向异性的关系等. 目前，b 值与应力的反比关系已经得到了研究人员的广泛认可与应用.

　　最常见的 b 值的计算方法是线性最小二乘法和极大似然法，在样本量足够大的情况下，两种方法计算结果的差别很小. 近年来，随着极大似然法的发展，国外已经极少使用最小二乘法. 影响 b 值计算结果的因素众多，包括地震目录的完整性、MC 与 ΔM 的选取与样本量 N 的大小等. 然而，构造应力可能是除了计算方法以外影响 b 值变化的最重要因素，其他因素仍然是次要的.

　　减轻地震风险的可能方法之一是通过对地震前兆的观测来预测即将发生的地震，地震前 b 值的时间变化是地震预测的重要前兆. 但是由于大震前 b 值的前兆增加或减少说明 b 值异常作为地震前兆具有多样性，因此，如何根据 b 值异常进行地震预测仍然需要深入研究.

　　b 值的空间分布可以用来准确预测破裂区域，异常低 b 值区指示高应力积累，能够判识强震危险性区. 另外，b 值的空间扫描结果还可作为判断未来强震危险性的一个指标，可以进一步运用在地震危险性评价研究中，因此，b 值空间分布方面的研究在中-长期的地震预测工作中有着十分重要的地位.——论文作者：孟昭彤，刘静伟，谢卓娟，吕悦军*