CMWPE结合SaE-ELM的轮对轴承故障诊断方法
时间:
摘要:针对 DF4 型内燃机车轮对轴承不同故障状态的判别问题,提出了一种基于复合多尺度加权排列熵(Composit Multiscale Weighted Permutation Entropy, CMWPE)和自适应进化极限学习机(Self-Adaptive Evolutionary Extreme Learning Machine, SaE-ELM)的机车轮对轴承故障识别方法。CMWPE 基于复合粗粒化和加权排列熵的思想,能很好地区分信号的不同模式。极限学习机的网络参数通过自适应进化算法进行优化,解决了 ELM 随机选取网络参数的局限性,提高了网络的泛化性能。计算机车轮对轴承不同健康状态下振动信号的 CMWPE,利用 SaE-ELM 识别轴承所属故障类型及故障程度。在机务段的 JL-501 轴承检测台上采集了七种不同健康状态的轮对轴承试件的振动信号数据。结果表明,CMWPE 特征提取效果优于 MPE 和 MWPE;SaE-ELM 模式识别效果优于参数不经优化的 ELM。所提方法能够有效诊断机车轮对轴承的不同故障,且故障识别率达到 100%。
关键词:机车轮对轴承;故障诊断;特征提取;模式识别;复合多尺度加权排列熵;自适应进化极限学习机
外界非平稳载荷和内部非线性因素使得轮对轴承的振动信号往往呈现出繁杂性和不规则性。常规的时频度量方法对这种不规则和非平稳信号的处理效果不佳 [1]。为了弥补这一不足,许多基于熵的复杂性度量技术相继被提出,且被广泛应用于故障诊断领域。然而,样本熵容易被序列中的异常值影响,波动性较大[2];近似熵处理结果的同一性差 [3]。文献[4]的分析结果表明,排列熵(Permutation Entropy, PE)可以识别轴承振动信号的突变性和随机性。然而PE只能反映单一尺度的时间序列信息,特征提取效果不理想。Wu等 [5]经过改进并提出多尺度排列熵(Multiscale Permutation Entropy, MPE)MPE具有较强的抗噪能力和较高的计算能力,可以有效地反映滚动轴承非线性动力学特性,解决单一尺度下提取信号信息的局限性问题。但是,MPE在实际应用中存在两个主要缺陷:1)MPE是基于PE计算的,PE仅在提取序数模式时保留序数结构,如果仅提取顺序结构,则幅值信息将丢失;2)时间序列的长度因粗粒化处理而变短,将导致MPE提取的信息不足,尤其是对于短时间序列而言[5]。为弥补PE的缺陷, Fadlallah[6]等研发出加权排列熵(Weighted Permutation Entropy, WPE)。文献[7]中又研发出多尺度加权排列熵(MWPE)来克服单一尺度分析的不足。但是,MWPE 仍然存在一些由WPE和粗粒化时间序列引起的问题。为了克服上述WPE和MWPE的缺点,Zheng [8]等研发出复合多尺度加权排列熵(Composit Multiscale Weighted Permutation Entropy, CMWPE)。CMWPE通过对时间序列的不同幅值赋以不同的权重,充分保留了原始的数据信息,从而得到更为精准的熵值特征。同时粗粒化采用复合构造的方式,降低原始序列长度对粗粒化时间序列的影响,避免时间序列因粗粒化变短而引起熵值突变 [8]。
智能算法近年来越来越广泛地应用于滚动轴承的故障诊断。张龙等[9]结合时序模型和自联想神经网络对齿轮进行性能退化评估。何园园等 [10]提出 ELMD 熵特征提取与参数优化的支持向量机的齿轮箱智能故障诊断方法。Huang 等 [11]研发出一种新型神经网络算法―极限学习机(Extreme Learning Machine, ELM),其效率高、拟合性能好且不易陷入局部最优。但由于 ELM 的隐含层节点在训练之前先指定,最终会导致获得的模型中存在某些对网络性能贡献较少的节点,造成模型结构的冗余,影响网络的性能。为弥补 ELM 的缺陷,Cao 等 [12] 研发出一种自适应进化极限学习机 (Self-Adaptive Evolutionary Extreme Learning Machine, SaE‐ELM)算法来寻找 ELM 网络参数的最优值。
基于以上分析,针对如何有效识别轮对轴承故障的问题,本文先用 CMWPE 提取机车轴承原始信号的特征信息,然后利用 SaE-ELM 模型对轴承不同故障类型和故障程度 进行智能识别。该方法结合了 CMWPE 精准表征信号非线性特征信息和 SaE-ELM 运算速度快、网络泛化性能好的优势。为验证本文方法的有效性,将真实工况下损伤的 DF4 型内燃机车轮对轴承用于本次实验研究。
1 复合多尺度加权排列熵方法
1.1 加权排列熵方法
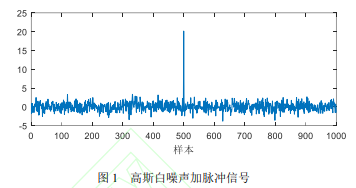
PE 具有理论简单、抗噪能力强等优势,因此在故障诊断领域应用较为广泛[13-14]。但 PE 只考虑了时间序列的序数结构,简单地将具有不同幅值的相同模式视为相等,而忽略了相同序数之间的幅值特性,其通常包含更重要的时间序列信息,这不可避免地影响熵的计算精度[15]。因此,文献[6]在 PE 的基础上,提出了 WPE,即在一般 PE 的基础上考虑了时间序列的幅值信息,通过引入加权因子,对相同序号下的不同幅值进行加权。为了说明 WPE 的优势,将脉冲信号加入到高斯白噪声中进行分析验证,如图 1 所示。
分别计算高斯白噪声加脉冲信号的 PE 和 WPE 值,根据文献[16]选择嵌入维数 m=6,时延 =1。如图 2 所示,可以看出 PE 的单调不变性,但 WPE 对幅值信息非常敏感。由此说明加权方法可以检测数据的突然变化,并为规则的尖峰模式分配更多的权重[6]。
1.4 对比分析
通过对 1/f 噪声和高斯白噪声两种噪声信号的分析,将 CMWPE 与 MPE 和 MWPE 进行比较,验证 CMWPE 的优越性并介绍 CMWPE 参数的选择过程。 CMWPE 中有 4 个参数需人为设定,分别为:尺度因子 s,样本长度 N,嵌入维数 m 和时延。其中,s 通常设置为 s>10,设定 s=20。m 对 CMWPE 有一定的影响,若 m 过小,过少的信息将无法全面表征时间序列所蕴含的原始信息;反之,若 m 过大,时间序列的微弱变化在熵值计算时易被忽略,且计算非常耗时。因此,通常设定 m 的取值范围在[4,7]之间,设置 m=6。时延影响较小,一般设定为 =1[17]。
由图 3 可知,1/f 噪声和白噪声的 CMWPE、 MWPE 和 MPE 值都随尺度因子的增加而单调减小。图 3(a-c)分别是 1/f 噪声的 CMWPE,MWPE 和 MPE,而图 3(d-f)分别是白噪声的 CMWPE,MWPE 和 MPE。比较图 3 中 CMWPE,MWPE 和 MPE 的误差棒图可以发现,MWPE 和 MPE 的标准偏差值随着比例因子的增加波动较大,而 CMWPE 的标准偏差值不随比例因子的增加而波动,CMWPE 曲线几乎保持平滑和稳定。
另外,由图 3(d-f)中长度为 2400 的 1/f 噪声和白噪声的 CMWPE,MWPE 和 MPE 曲线图可以看出, CMWPE 可以在任何尺度上区分这两种噪声,而这两种噪声的 MPE 和 MWPE 在某些尺度上有重叠。表明 CMWPE 的整体稳定性优于 MWPE 和 MPE。此外,对于相同的尺度因子,白噪声的 CMWPE,MWPE 和 MPE 值始终大于 1/f 噪声,这表明白噪声比 1/f 噪声更不规则。
由图 3 还可以观察到,当 N 较小时,1/f 噪声和白噪声的 CMWPE 具有较大的偏差,并且当 N 较大时偏差将减小。另外,文献[3]的研究表明,时间序列长度应满足 N>200s,但随着 N 的增加,偏差减小的效果有限,且计算量呈指数增加。设置样本长度 N=4800。
3 实验分析
3.1 诊断模型
本文所提方法如图 5 所示,主要步骤如下:
(1)采集信号。采集真实工况下不同损伤状态的轮对轴承的原始加速度信号,采样频率为 s f 。
(2)预处理数据。归一化处理样本数据,除去其中的奇异值,以免影响识别精度。
(3)提取故障特征。利用 CMWPE 算法对不同健康状态的轮对轴承振动信号进行特征提取。
(4)建立模型。初始化网络,通过 SaE 寻找 ELM 网络的最佳参数。
(5)分类识别。利用训练好的 SaE-ELM 模型对轮对轴承的故障类型进行识别。
3.2 实例分析
实验所用的真实工况下损伤的轴承试件如图 6 所示。所用轴承均是从 DF4 型内燃机车上拆卸下来的实际机车轮对正常和故障轴承。实验前。实验过程中,轴承由图 7 所示的 JL-501 型轴承检测台驱动。检测台主要由台身、电气系统、液压系统和主轴箱组成。主轴转速范围为 120~1200 r/min。
本文利用该检测台对机车轮对轴承进行驱动和加载,转速为 500 r/min、径向外载为 1.4 MPa。利用三个型号为 CA-YD-187T 的加速度传感器和型号为 NI.USB-4431 的采集卡完成机车轮对轴承振动信号的采集,采样频率 s f 为 20000Hz。
表 1 给出了正常及图 6 所示的六种故障状态共七种轮对轴承的状态信息和样本数量,机车轮对轴承的状态标签依次设为 1-7。采集真实工况下损伤的轴承试件的加速度振动信号,各为80 组,样本长度为4800。图 8 为轴承不同故障类型的时域信号。
3.3 特征提取
把不同嵌入维数(m 分别设置为 4,5,6,7)下的 CMWPE 应用于两种状态轴承数据的分析过程中,如图 9 所示。据图 9 可知:当嵌入维数 m 较小(为 4 或 5)时,CMWPE 熵值拟合线较为平缓,多尺度的优势无法体现,特征区分不明显;而当 m 较大(为 7)时,时间序列的细微变化易被忽略,导致两种状态熵值曲线较为接近,无法有效区分故障类型,且大大增加计算量,效率低下。因此,本文选取 m=6 较为合理。
计算出具有不同故障类别和程度的机车轮对轴承的所有 560 个振动信号样本的 CMWPE 值,如图 10 所示。从图 10 中可以发现正常轮对轴承的 CMWPE 值从尺度 3 到 5 逐渐增加,从尺度 5 到 20 逐渐减小。对比于正常轴承,故障轴承的振动信号的总体趋势在不同的比例因子下具有不同的波动。当机车轮对轴承处于正常状态时,信号振动状态更为复杂,信号更无规则,规律性低,蕴含了更多的特征信息,故熵值较大;而当出现故障时,振动信号的波动较为规律,自相似性高,故熵值较小。表明不同的故障使得振动信号的复杂性在一定范围内有所不同,这也使得区分各种故障和故障程度成为可能。例如,轮对轴承在状态 2、3 的振动信号在比例因子为 5 到 10 时的 CMWPE 一直下降,但当比例因子为 10 到 12 时,CMWPE 将单调增加。当比例因子为 3 到 5 时,轴承在状态 7 的 CMWPE 增大,而当比例因子大于 5 时 CMWPE 的整体性能逐渐降低,且熵值较小。因此,CMWPE 可以有效地区分滚动轴承故障部位和程度。
此外,不同机车轮对轴承振动信号的 CMWPE 值在第 20 个尺度时基本没有交叉重叠,区分较为明显。若选择超过 20 个尺度的 CMWPE,易导致信息冗余,影响故障的识别精度;而若选择较小尺度的 CMWPE,故障信息则无法完全被提取,故障识别率低。
3.4 模式识别
SaE-ELM 的建立首先要求设定相关初始网络参数。输入特征向量 CMWPE,由表 1 可知每种轴承状态有 80 个样本,训练样本为 40 个,剩下的作为测试样本。
将 RMSE 设为 SaE 的适应度目标值。变异因子设为 0.5、交叉率设为 0.3、变异策略选择策略 3、种群个数设为 100 且 ELM 隐含层节点数设为 10。通过比较每类函数所获得的最佳测试结果选择激励函数,将表现更优的 Sigmod 作为激活函数。
以上述参数训练 SaE-ELM 模型,并将训练后的 SaE-ELM 模型用于测试样本的智能识别。模型对 280 个测试样本的 10 次平均识别准确率达到 100%,由实验可知, =20 时,CMWPE 能够有效地提取机车轮对轴承的故障特征,SaE-ELM 模型对不同故障及不同故障程度能很好区分。
3.5 方法对比
将 CMWPE 值输入到 ELM 模型中进行分类识别,得到 10 次平均分类准确率为 98.57%。再将 MWPE 值输入到训练好的 SaE-ELM 模型中,得到 10 次平均准确率为 87.14%。最后将 WPE 值输入到 SaE-ELM 中,得到 10 次平均准确率为 73.57%。不同方法的故障诊断准确率结果如表 2 所示,显然,本文所提的故障诊断方法准确率最高,验证了本文方法的优越性。
4 结论
本文针对 DF4 型内燃机车真实工况下损伤的轮对轴承的故障类型的判别问题,提出了一种基于 CMWPE 特征提取与 SaE-ELM 故障识别的诊断方法。计算机车轮对轴承不同健康状态下振动信号在 20 个尺度上的 WPE 构成 CMWPE 特征向量,输入到训练好的 SaE-ELM 模型中进行智能故障识别。结果表明, CMWPE 能全面准确地表征机车轮对轴承振动信号在不同尺度下的复杂度,并且 SaE-ELM 模型可以很准确且高效地识别机车轮对轴承的不同故障及不同故障程度。通过对机车轮对轴承试件振动信号的诊断分析,可以得出以下结论:
(1)采用一种能全面提取非平稳时间序列特征信息的方法—复合多尺度加权排列熵,弥补了排列熵幅值信息易丢失和多尺度排列熵粗粒化的固有缺陷;利用SaE对ELM的网络参数进行寻优,解决了ELM随机选取网络参数的局限性,提高了网络的分类识别性能。实验结果表明,所提特征提取方法优于MWPE和WPE, SaE-ELM模式识别效果优于ELM。
(2)提出一种基于CMWPE和SaE-ELM的机车轮对轴承故障智能识别方法。实验表明,该方法识别准确率达到100%,为提高轮对轴承故障的检测精度和效率提供了一种有效的方法。——论文作者:张龙1,彭小明1,熊国良1,吴荣真1,胡俊锋2
[参考文献]
[1] Zhang C L, Liu Y L, Wan F Y, et al. Adaptive filtering enhanced windowed correlated kurtosis for multiple faults diagnosis of locomotive bearings[J]. ISA Transactions, 2020, 101: 421-429.
[2] Wu S D, Wu C W, Humeau-Heurtier A. Refined scale-dependent permutation entropy to analyze systems complexity[J]. Physica A: Statistical Mechanics and its Applications, 2016, 450: 454-461.
[3] Zhang L, Xiong G, Liu H, et al. Bearing fault diagnosis using multi-scale entropy and adaptive neuro-fuzzy inference[J]. Expert Systems with Applications. 2010, 37(8): 6077-6085.
[4] Zhou J Z, Xiao J, Xiao H, et al. Multifault diagnosis for rolling element bearings based on intrinsic mode permutation entropy and ensemble optimal extreme learning machine[J]. Advances in Mechanical Engineering, 2014, 6: 485–520.
[5] Wu S, Wu P, Wu C, et al. Bearing fault diagnosis based on multiscale permutation entropy and support vector machine[J]. Entropy, 2012, 14(8): 1343-1356.
[6] Fadlallah B, Chen B, Keil A, et al. Weighted-permutation entropy: a complexity measure for time series incorporating amplitude information.[J]. Physical review. E, Statistical, nonlinear, and soft matter physics, 2013, 87(2).
[7] Yin Y, Shang P. Weighted multiscale permutation entropy of financial time series[J].Nonlinear Dynamics, 2014, 78(4): 2921–2939.
[8] Zheng J D, Dong Z L, Pan H Y, et al. Composite multi-scale weighted permutation entropy and extreme learning machine based intelligent fault diagnosis for rolling bearing[J]. Measurement, 2019, 143: 69-80.
[9] 张龙,成俊良,杨世锡,等. 基于时序模型和自联想神经网络的齿轮故障程度评估[J]. 振动与冲击. 2019, 38(2): 18-24 (in Chinese) Zhang L, Cheng J L, Yang S X, et al. Fault severity assessment for gears based on AR model and auto-associative neural network[J]. Journal of Vibration and Shock, 2019, 38(2): 18-24.
[10] 何园园,张超,朱腾飞. ELMD熵特征融合与PSO-SVM在齿轮故障诊断中的应用[J]. 机械科学与技术, 2019, 38(2): 271-276.


