洪水工况下某尾矿坝溃坝试验研究
时间:
摘要:为探究洪水工况下某尾矿坝的溃坝形式及其破坏发展过程,开展了1:100的大比尺物理模型试验,并进行了数值模拟试验。模型试验表明尾矿坝的溃坝形式为渗透破坏,其破坏表现形式为流土。模型试验显示浸润线上升的速率先快后慢。停止抬升水头后,由于滞后作用,浸润线在一段时间内仍然会小幅上升。浸润线在坝面出溢的顺序为:第二级子坝—第三级子坝—第一级子坝—第四级子坝。数值模拟得到了与模型试验一致的结果,尾矿坝稳定性分析得到坝体在上游水头为125m时仍未发生失稳破坏,符合模型试验的观测现象。尾矿坝最终将因流土破坏发展至坝顶产生决口而引发溃坝。大型模型试验法与数值模拟方法相结合研究洪水工况下尾矿坝溃坝问题,可弥补单一研究方法的局限性,分析结果更可靠。
关键词:安全工程;尾矿坝;洪水;模型试验;渗透破坏;数值模拟
0引言
尾矿坝是金属、非金属矿山为了堆存尾矿而建立的一种形似堤坝的构筑物。尾矿坝的安全运行一直是矿山及政府部门的关注重点,这种特殊的水工构筑物一旦发生溃坝事故,高势能顺势转化为巨大的动能,将会造成大量的人员伤亡、财产损失和环境污染,甚至对当地的经济发展与社会稳定带来长期的不利影响[1]。2008年我国山西省襄汾县平硐尾矿坝发生了一起特别重大溃坝事故,事故外泄容量26.8万m3,过泥面积30.2公顷,冲击下游大片民用区域,致使277人死亡,直接经济损失高达9619.2万元[2]。
研究尾矿坝溃坝机理,对于了解大坝溃决发生、发展过程,掌握溃坝泥石流对下游的破坏范围及程度,以及编制应急预案、组织撤离与逃生、实施紧急救援等,均具有重大意义[3,4]。在对尾矿坝的溃坝问题研究中,其溃决机理由于涉及到水文地质、坝体结构、筑坝材料以及施工质量等诸多因素而尤为复杂[5,6]。ShakesbyRA等[7]于1991年对Arcturus金矿尾矿坝溃坝进行研究,分析了溃坝发生的主要原因,为后来学者探究尾矿坝溃坝机理、提出科学的尾矿坝管理方法奠定了基础。Wu等[8]利用尾矿库物理模型研究分析了尾矿坝溃坝过程中泥砂的运动特性,并提出了相应的防护措施。Kamrul等[9]更新了尾矿库溃坝的数据库,从全球角度分析了近百年尾矿库溃坝的影响。李全明等[10]于2008年对尾矿坝溃坝路径和溃坝模式进行研究,得到了可能的溃坝路径和5种溃坝模式,建立了尾矿库溃坝风险指标体系。吴宗之等[11]统计、分析了国内外160起尾矿坝事故,利用鱼刺图分析法研究了溃坝发展过程及其成因。周科平[1]从尾矿坝溃坝灾害的形成发育过程入手,构建了五种常见的尾矿坝溃坝灾害链模型和复杂灾害链网。
不考虑设计构造缺陷,尾矿坝溃坝的主要原因有洪水漫顶、渗透破坏、边坡滑移、坝基失稳及地震液化五类[12]。其中,由渗透破坏和洪水漫顶导致的溃坝占尾矿坝溃坝事故总比例的80%,洪水漫顶与渗透破坏在尾矿坝事故中的高占比也揭露了水对尾矿坝稳定性的重要影响[13,14]。而这两种破坏形式多发生于汛期,且每次溃坝前都有一定的先兆,如管涌口、裂缝及决口的产生[15]。因此,有必要探究洪水工况下尾矿坝的溃坝形式及机理、掌握其溃坝的发展过程、分析坝体的稳定性,从而科学、合理的对尾矿坝进行监测、管理,确保其正常运行[16]。本文开展了1:100的大比尺尾矿坝溃坝模型试验,并结合数值模拟探究了洪水工况下的某尾矿坝溃坝形式及其破坏发展过程。模型试验真实还原了洪水工况下某尾矿坝坝体稳定性的动态变化趋势,反映了尾砂的运动规律和演变过程。数值模拟试验解释了坝体内部渗流场、应力场在时间、空间上的分布规律。两者相结合的方法以期为理论分析和工程实际提供依据和试验数据,指导尾矿坝的安全管理以及防灾减灾工作。
1尾矿坝大型溃坝模型试验
1.1尾矿坝原型概况
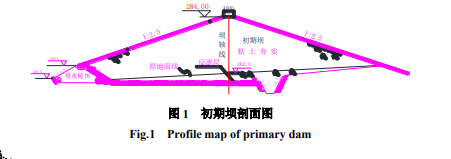
原型尾矿坝为一座钨矿尾矿坝,位于江西省赣州市某县一个南北走向的狭长山谷内,两岸山体坡度较陡,坡角一般为20º~40º。库长约1.8km,平均宽度约400m,汇水面积2.5km2。初期坝为粘土心墙风化料坝,坝顶高程284.00m,坝底高程262.00m,坝高22m,坝长75m,坝顶宽4m,上下游坡比1:2.5(图1)。坝基基岩为砂岩、板岩和闪长石英岩,基岩以上的覆盖层在两岸部分为厚0.5~2m的砂土,在沟底河床部分为厚5~6m的第四纪冲积砂卵石层。
尾矿堆积坝采用上游式筑坝,现堆积坝顶高程约315m,坝高53m,已堆积库容约559×104m3。堆积坝平均外坡比为1:4.9,307m标高以上堆积边坡1:3.8。尾矿堆积坝的设计平均外坡比为1:5,尾矿沉积滩平均坡度为5%,设计最终尾矿堆积坝标高为368.00m,总坝高106.00m,总库容1550×104m3,服务年限为65年。该库目前属四等库,防洪标准按200年一遇设防。后期属二等库,防洪标准按1000年一遇设防。
1.2物理模型的制作
1.2.1模型砂选取
模型试验重点关注坝体变形过程中颗粒运动的积聚效应,初期坝由粉质粘土堆筑,堆积坝采取矿山原型尾砂,对其进行筛分后作为模型砂堆筑坝体。图2为模型砂的粒径累计曲线,该曲线较陡,表明土粒较均匀,且颗粒较粗。计算得到模型砂的不均匀系数Cu为2.29,曲率系数Cc为0.84。一般认为Cu<5或Cc在1~3以外的砂类土属于级配不良土,则判定模型砂为级配不良土。根据前苏联学者伊斯托美娜提出的不均匀系数判别法,初步判断模型砂归属为流土型土。
1.2.2模型概况
在几何相似条件下按原型尾矿坝二等库的级别开展1:100的大比尺尾矿坝物理模型试验,模型制作尺寸为12m×7m。整个尾矿坝模型由四部分组成:基岩、坝体、观测系统及供水循环系统。具体的步骤为:根据原型尾矿坝的地形地势及高程信息,在Civil-3D建模软件中建立了相应的三维实体(图3);然后在实体中横向等距提取出若干个地形剖面,根据剖面的高程及相对位置按1:100缩小比例用钢管结构制作出全部断面,并将防水布盖于钢架群上模拟出基岩全貌(图4);根据矿山提供的初期坝图纸和确定的比尺,采用粉质黏土制作初期坝;再将从矿山尾矿坝运回的尾砂进行筛分搅拌均匀制备成体积浓度为30%、可自由流动的尾矿浆,采用矿山常用的管线法模拟放矿,用分层填筑法一级一级地堆筑坝体至设计标高。堆筑坝体过程中在指定位置埋入四支孔隙水压计,即每堆筑一级子坝,埋设一支孔隙水压计,四支孔隙水压计埋设的位置分别定义为位点一、二、三和四(图5)。
1.3溃坝试验
1.3.1溃坝现象
试验采取间歇性向库内注水的方式模拟洪水工况,注水时保持流量稳定,整个试验过程中排渗管保持开启状态。开始注水的时刻作为试验开始时刻,整个溃坝试验历经448min,图6为坝体破坏各阶段的典型图片。试验结果显示:在库内的水漫顶之前,尾矿坝坝体已发生渗透破坏,即溃坝形式为渗透破坏。具体的尾矿坝变形发展事件如下:
试验第138min,第二级子坝右端与基岩接触带处最先出现渗水(图6a),数分钟后溢流区即扩展至第二级子坝的整个坝面。第174min,第三级子坝也出现溢流(图6b),局部溢流区发生在左侧。第190min,浸润线在第一级子坝出溢。第233min,在第二级子坝右端出现了一条湿陷裂缝,第236min,此处发生了第一处流土破坏(图6c),破坏表现形式为流滑。第239min,第一级子坝左侧发生了第二处流土破坏,破坏形式与第一处相同。第248min,坝体左右两侧的流土破坏区已形成了冲蚀沟(图6d、6e)。冲蚀沟相当于一个局部渗透系数较高的区域,此处渗流水有较大的速度矢量,优势流发展迅速,对流沙的裹挟将使局部危害加剧,更容易引发后续的渗透破坏。第292min,流土破坏已向上游侵蚀至第三级子坝(图6f)。第303min,第三级子坝左侧发生了第三处流土破坏(图6g)。第332min,在水力侵蚀的迅速发展下,左右两侧的破坏区已形成了两条水沟,沟中水流不间断,裹挟着细砂,且肉眼可见渗流水的流动与流径。第348min,第四级子坝也呈现沼泽化(图6h)。第448min,流土破坏区侵蚀至第四级子坝,视为整个坝体破坏(图6i)。经测量,坍塌区最深约12厘米,宽度最大约80厘米。需要指出的是,尽管尾矿坝发生大面积的渗透破坏,但坝体仍未发生失稳滑坡,流土破坏区发展至坝顶产生决口,最终引发尾矿坝溃坝泄洪。
1.3.2孔隙水压及浸润线变化规律
模型试验过程中采集得到的孔隙水压力数据变化分为5个增长阶段,如图7。在库水位间歇上升的过程中,孔隙水压分阶段增长。除位点一以外,其余三个位点的孔压增长趋势大体一致。在第一个阶段,位点二、三、四均经历了孔压线性增长—增长陡缓—平稳的变化过程。从第二个阶段开始,位点三的孔压在每次增长速率变缓后,出现一个近似线性的下降趋势,且每一阶段都比上一阶段下降的速率更大。位点四从第三阶段开始出现下降的趋势,但下降的形态无规律。孔压的下降是由于在停止抬升水头后的一段时间内,持续的渗流运动在不断地损耗水头,导致某些单元内渗流的流出量大于流入量。而位点二距离库内相对较远,滞后作用的时间更长,故在停止蓄水后一段时间内仍能保持孔压稳定。位点一由于离上游最远、离排水管最近,对库水位的变化不敏感,孔压上升较慢,孔隙水压仅在第二阶段出现明显的线性增长,然后保持平稳,在第三阶段有较小增长,而后基本保持平稳。
相关知识推荐:水利工程师论文投稿的核心期刊
根据图7中孔隙水压的变化规律,选取若干个时间点,绘制出这些时刻的坝体浸润线,如图8。结果显示,浸润线埋深随上游水头的升高而变浅。停止抬升水头后,由于滞后作用,浸润线在一段时间内仍然会小幅上升。如果库水位长时间未得到补给,在排渗正常的情况下,浸润线将降低。在蓄水前期,坝体大部分处于非饱和状态,土体基质吸力大,浸润线上升得快;蓄水后期,坝体饱和度增加,基质吸力降低,浸润线上升缓慢。
2数值模拟试验
2.1模型构建与前处理
采取Midas/GTS有限元分析软件对该尾矿坝进行渗流和应力耦合作用下的稳定性分析。以三维尾矿坝模型中轴线剖取出的断面作为二维数值模拟的典型断面,参照原型尾矿坝的钻孔资料将模型概化分层[17],如图9。该计算模型长1046m,高126m。选取莫尔—库伦模型作为分析求解的本构模型,各土层的物理力学参数见表1,渗透系数见表2,分析过程中考虑土体的非饱和特性。对计算模型采取三角形+四边形网格划分,共生成11742个单元,35439个节点,如图10。水头边界条件按1000年一遇的来洪流量施加,同时考虑排渗管的正常运作。
2.2计算结果分析
2.2.1渗流场
图11(a-e)呈现了库水位为100m、110m、120m、123m及125m时的坝体浸润线图。图11(b)中,浸润线在第二级子坝处埋深较浅,离坡面仅7m,此时浸润线的最小埋深已超出规范的安全阈值,对坝体安全是不利的[18]。图11(c)中,坝体浸润线已与第二级堆积坝坡面相交,即浸润线最先在第二级堆积坝出露,此时若未能及时降低浸润线,则可能会因渗透失控而导致坝体破坏。继续抬升水位至123m,浸润线与第三级堆积坝相交,并与第一级堆积坝坝顶贴近。当上游水头涨至125m时,浸润线与第一、四级堆积坝均相交,在整个坝面出露。结合模型试验的结果,可知数值模拟所得的浸润线变化规律与试验现象是吻合的,即浸润线随着库水位的上升而升高,且在坝面的出露顺序为第二级子坝—第三级子坝—第一级子坝—第四级子坝。
2.2.2应力场
为了方便分析,在图12中所示提取五个参考单元,单元号28658、45708、31968、31924、42167,分别命名为点A、B、C、D、E。
在上游水头为100m、110m、120m、123m、125m的工况下,坝体的平均有效应力分布见图13(a-e)。其最大值始终位于横剖面中部的最底端(云图中红色区域),最小值处在坝体沉积滩处(云图中深蓝色区域)。在同一工况下,土体的有效应力随着埋深的增大而增大,即由坝面到基岩逐渐增加,符合应力分布规律。在库水位不断上升的过程中,模型整体的平均有效应力呈下降的趋势,其最大值由952.2kN/m2降至732.2kN/m2(表3),这是由于坝体在从非饱和到饱和的过程中,其孔隙水压力逐渐增大,引发了更大的浮托力,而导致土体的有效应力降低。应力参考点的数据变化也反映了此规律,具体数值见表4。
2.2.3稳定性判断
利用强度折减法(SRM)计算得到的各洪水工况下尾矿坝的安全系数见表5。结果显示,尾矿坝的安全系数随着库水位的增长而下降。上游水头由100m涨至125m后,安全系数由1.726降至1.256,降幅27.23%。根据《尾矿坝设施设计规范》(GB50863-2013),坝体最终还是稳定的[18]。但是判断边坡是否发生失稳破坏,对于强度折减法计算的结果而言,应进一步考察:数值计算是否收敛;位移是否有大的突变;塑性区是否贯通。
首先,根据计算脚本,有限元计算是收敛的;其次,各参考点的位移变化并未出现大的突变,具体数值见表6;最后,取水头123m与125m工况下的有效塑性应变云图进行分析,图14(a-b)中两种工况下的塑性区都未出现在坝体坡面或坡顶,更不存在贯通。因此,可以判断该尾矿坝模型在水位即将漫顶时未发生深层滑移,即坝体的骨架结构是稳定的。结合物理模型试验分析,在坝体浸润线到达第四级子坝坝面之前,尾矿坝已经发生了渗透破坏,但是坝体并未发生结构失稳。从这一点来看,数值模拟的结果和物理模型试验的现象是相符的。之后随着流土的发展,坝体的破坏区不断向坝顶延伸,最终将使坝顶产生决口而引发溃坝泄洪。
3结论
(1)尾矿坝在洪水工况下的溃坝模式为渗透破坏,其表现形式为流土。整个试验过程分为两个阶段,第一阶段为渗流稳定阶段,即溢流水清澈,坝体表面稳定,无颗粒的移动;第二阶段为流土发展破坏阶段,土体中不断发生着渗透变形,损失了较多土方量,两阶段各占试验时长的二分之一。流土破坏始于坝体的薄弱地带—与基岩的交界处。破坏的发展表现为多种形式,这些形式单独或同时发生。流土破坏初期,坝面会产生多个砂沸点,并相继出现湿陷裂缝,这些可作为渗透破坏的警兆。
(2)浸润线上升的速率先快后慢。停止抬升水头后,由于滞后作用,浸润线在一段时间内仍然会小幅上升。如果库水位长时间未得到补给,在排渗正常的情况下,浸润线将降低。由此可知,在来洪前,应对排渗设施进行排查检修,保证其运作良好。洪水期,应采取必要措施增强排洪力度,降低浸润线,避免尾矿坝发生渗透破坏。
(3)数值模拟的结果与物理模型试验的结果吻合良好,并进一步解释了坝体内部渗流场、应力场在时间、空间上的分布规律。基于强度折减法(SRM),得出当上游水头为125m时坝体仍未发生失稳破坏,与模型试验的结果一致。
(4)数值模拟方法无法实现尾矿坝渗透破坏的模拟,而大型物理模型试验可以观测到该现象,因此,采用大型物理试验和数值试验相结合的方法研究洪水工况下尾矿坝溃坝问题可靠性更高。——论文作者:何文1,2,3,陈豪1,2,郑场松1,2,汤紫凯1,2,林凤翻1,2

 >
>