量子错误缓解研究进展
时间:
摘要由于与环境的相互作用及对量子设备的控制中存在的偏差,量子设备总是在不断产生错误.若不对这些错误加以处理,错误的积累会使得量子算法的实施变得毫无意义.成熟量子计算机的实现依赖于量子纠错技术以纠正量子设备中的错误.然而,由于量子纠错开销巨大,其难以在近期量子设备中实现.故在有噪声中等尺寸量子时代,以变分量子求解器为代表的量子算法选择量子错误缓解技术来压制错误,而非纠正它们.量子错误缓解允许仅通过中等大小的额外资源获得可以接受的计算精读,并已在理论及实验上展示出其可行性.旨在介绍与总结量子错误缓解领域的最新进展,并展望该技术未来发展的前景与方向.
关键词量子计算;近期量子设备;量子错误缓解;量子算法;有噪声的中等尺寸量子时代
近期量子设备的特征限制了能够操控的量子比特(qubit)数目,一般为几个到几十个量子比特,且存在一定的噪声,因此称之为有噪声的中等尺寸量子(noisyintermediate-scalequantum,NISQ)设备[1].由于能够控制的量子比特数目有限,故一般无法使用量子纠错码将物理量子比特编码为逻辑量子比特后进行计算:据估计,以合理的成功概率实现超越经典计算机算力的Shor算法需要将几千个物理量子比特编码为1个逻辑量子比特[2].故而,对于NISQ设备我们需要考虑设计对其友好的算法,并在此基础上设计算法能够成功实施的相应技术.一系列面向NISQ设备设计的算法已经提出,其中最受瞩目的为变分量子求解器(variationalquantumeigensolver,VQE)[3-5]和量子近似优化算法(quantumapproximateoptimizationalgorithm,QAOA)[6],前者多用于量子模拟(quantumsimulation)领域[7],而后者主要面向计算机领域的组合优化(combinatorialoptimization)问题[8].与此同时,量子错误缓解(quantumerrormitigation,QEM)技术[9]成为NISQ时代在量子设备上可靠地实施算法的必不可少的元素.
2019年和2020年,Google公司在量子计算领域取得了里程碑式的进展,分别在其Sycamore量子芯片上实现了量子霸权(quantumsupremacy)实验[10]和目前在量子计算机上实现的最大的量子模拟(quantumsimulation)算法[11].对于后者,依赖于后处理(post-selection)和McWeen纯化(McWeenpurification)的量子错误缓解技术,研究人员们成功将保真度(fidelity)最低2%的计算结果还原到99%,足以体现量子错误缓解对于NISQ时代量子计算的重要性.
本文主要以面向VQE算法实施的量子模拟算法为背景,介绍相关的量子错误缓解技术.
1量子模拟和变分量子特征求解器简介
量子力学是描述微观世界的基础理论.通过经典计算机研究量子系统问题是物理、化学、材料等领域的重要研究方向之一.然而,随着系统自由度的增加,经典计算机所需要的计算资源在最一般的情况下呈指数级上升,称之为“指数墙”(exponentialwall)困难[12].
意识到这一困难,Feynman最早于1982年提出了量子模拟的概念:通过可控的、易获得的量子系统来模拟难以获得的目标量子系统[7].直觉上,利用量子系统本身自由度指数级增大的希尔伯特空间(Hilbertspace),我们可以在一定程度上解决指数墙困难.
在量子多体物理和量子化学领域中,系统在低能态表现出的特性是研究人员关心的问题之一.其中,最具代表性的即为原子或分子系统的电子结构问题.电子结构问题的研究目的为对特定哈密顿量(Hamiltonian)H描述的原子或分子系统,理解其在低能态下相互作用的电子在原子核产生的势能下是怎样分布的.系统的性质由波函数(wavefunction)描述,电子结构问题要求我们求解系统的基态(groundstate)和低能激发态,并计算各个观测量的大小,其中最为重要的观测量为系统能量E.
Rayleigh-Ritz变分法给出了对量子基态求解的可行策略,其主要通过设定参数化的试探波函数(trialwavefunction)|ψ(θ)?,又称拟设(ansatz),θ为其参数.以能量E作为观测量为例,系统基态能量E0
可以看到,系统的基态能量给出了该观测量的下界,我们可以不断调整、优化拟设的参数使其逐渐逼近系统基态,从而获得基态能量.借助这一思想,VQE算法通过在量子计算机上制备试探波函数,通过测量获得观测量当前值,并使用经典计算机优化试探波函数参数实现对基态能量的求解.其优势在于利用量子计算机指数级增长的希尔伯特空间来表示波函数,经典计算机的参与减少了对量子线路(quantumcircuit)深度的要求.随着量子线路深度的增加,随机错误的数量和退相干(decoherence)效应的影响会越来越明显,故VQE算法保持较为浅层的量子线路深度的特性使其适合于在近期量子设备上实施.另外,VQE算法本身具有一定的对连续错误的缓解效果[4-5].当然,浅层量子线路的错误仍然会带来计算的偏差,本文将接下来总结针对浅层量子线路的量子错误缓解方法.
2量子错误缓解基本框架
本节主要讨论针对NISQ设备噪声的量子错误缓解方法.由于噪声的影响,我们考虑量子混态(quantummixedstate),而非纯态(purestate).考虑量子门"(·)=U(·)U?.设#为噪声信道(noisechannel),则有噪声的量子门为#?".这里,我们假设量子门实施中产生的错误为马尔可夫的(Markovian),即噪声信道与量子门的类型及施加位置等特征无关.
量子错误缓解则面向近期量子设备,提出了一种开销小、鲁棒性高的策略.与量子纠错不同,错误缓解不考虑实时地减少量子线路中的错误,而是仅考虑通过有噪声的测量结果?O?noisy=tr(ρnoisyoutO)恢复理想线路的理想测量结果?O?ideal=tr(ρidealoutO),如图1所示.对于近期量子设备实施的算法而言,例如第1节讨论的VQE算法等,其量子线路较浅,即便错误在算法实施过程中不断积累,我们依然可以以高概率恢复得到观测量的概率分布,代价是错误缓解算法会导致恢复得到的概率分布的方差增大,从而增加需要的测量样本数量.由于量子错误缓解技术不纠正错误,错误仍然会在线路中积累,故而,该技术仅在物理错误概率较低时起作用,且无法规模化到较深层的量子线路.
3量子错误缓解的主要方法
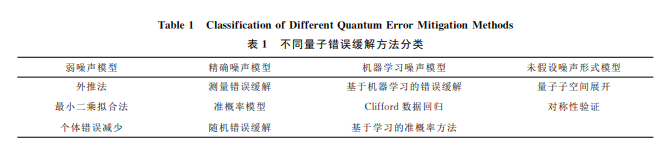
本节将具体介绍10类量子错误缓解方法以及各类方法相互结合的方法.根据对噪声模型的依赖程度和错误缓解的不同方法,我们将这些方法归为如表1所示的4种类型:弱噪声模型、精确噪声模型、机器学习噪声模型、未假设噪声形式模型.最后,我们将讨论各个方法间的组合方法.
3.1外推法
外推法(extrapolation)利用不同的物理错误率下运行相同的量子线路,从而通过不同错误率对应的测量结果外推得到无错误情况下的观测结果,如图2所示:
3.4对称性验证
当系统遵循一定的物理对称性时,我们可以通过设计满足这种对称性的波函数拟设来缩小参数搜索的范围.例如,对于遵循粒子数和自旋守恒的系统,考虑设计由使得系统的总粒子数和自旋守恒的幺正变换构成的波函数拟设,则可以选择幺正偶合簇(unitarycoupled-cluster)[21]方法,或者特定的硬件高效拟设(hardware-efficientansatz)[22].相应地,我们可以通过对称性检验(symmetryverification)[23-24]的方式来检验输出波函数是否仍然具备这种对称性.理想的量子算法实施会保持量子态的对称性,但是由有噪声的量子线路制备得到的量子态可能会破坏这种对称性.因为对称性仅在错误出现的情况下才会被破坏,故对称性验证方法的工作原理为丢掉对称性被破坏的测量结果.
相关知识推荐:计算机研究与发展是什么水平
具体而言,对称性检验量子线路输出态是否遵循特定对称性的方式为对该对称性实施奇偶校验,注意到该校验方式在量子纠错码中常常使用,但这里我们不纠正错误,而是去掉有瑕疵的结果.我们可以通过泡利群(Pauligroup)PPN来理解奇偶验证.泡利群PPN中所有元素由所有长度为N的泡利矩阵X,Y和Z,及单位矩阵I构成的直积态组成,群元的第i个元素代表作用到第i个量子比特的操作。
参考量子纠错中应用最为广泛的稳定子编码(stabilizercode),McClean等人[26]设计了对应的经典后处理版本,相较于稳定子编码需要对稳定子群(stabilizer)中各生成元(generator)实施对应的奇偶校验线路,该方法可以在完全忽略这些线路实施的情况下检测错误.另外,我们可以以概率的形式实施量子纠错码中具备的各个对称性投影,使得量子态回归到码字(codeword)空间.相应的后处理解码器(decoder)通过数值实现了对5个量子比特量子化学模拟的纠错并获得了50%的有效纠错阈值(threshold).
3.5测量错误缓解
测量错误缓解(measurementerrormitigation)[27-29]用于减少测量过程中的错误.假设理想测量过程由一组正算符值测量(positive-operatorvaluedmeasure,POVM)构成{Fi}.
4量子错误缓解技术未来发展方向
以测量错误减少和准概率方法等为代表的错误缓解技术,面向特定的量子信道,通过严格推导可以达到对错误形成有保证的缓解效果.然而,实践过程中,一方面,这类方法依赖错误的形式,故需要实施具有高开销的态和信道层析技术;另一方面,真实设备中错误的来源多种多样,很难通过严格的推导实现对所有类型错误的缓解.而类似于外推法等方法,没有利用错误本身的信息,导致达到理想精度的错误缓解效果一般需要高度的计算资源.机器学习算法为这种两难的困境提出了一大出路.理由是机器学习算法具有强大的模式识别的能力[39],能够从训练数据中学习到系统噪声对理想测量期望值的改变模式,故使得机器学习算法在这一方面具有更高的灵活性:既可以用于各类特定形式的量子信道中,也可以对实验数据进行处理.故而,未来在量子错误缓解领域更多机器学习算法的进入值得期待.并且,机器学习算法的开销主要集中于训练阶段,当完成训练后可以使用训练好的模型低成本地推断各类情况下的错误缓解结果.
除此以外,利用计算任务本身特性的错误缓解算法展现出具有优势的表现,如3.6节的N阶可表示性[31].在近期量子计算任务中,量子模拟求解化学、物理体系的基态及动力学过程等成为最受瞩目的分支之一,值得期待的是未来更多面向特定物理、化学体系的错误缓解算法的提出.这有赖于在传统凝聚态物理、量子多体物理和量子化学领域对体系的知识积累,利用相应的认识和见解,可以获得理想结果所存在的子空间,从而对量子态施加除了对称性验证以外更为具体的限制以约束结果到相应子空间.可以预见,对物理、化学体系信息的更充分利用可以带来更加稳定的结果表现以及在算法开销上的优势.
5结束语
我们通过量子模拟,引入和介绍了量子错误缓解技术的重要性:在NISQ时代,通过插入特定量子门到量子线路中和经典后处理,量子错误缓解保证了即便存在噪声,较浅量子线路也可以有效实施.并且,量子错误缓解方法可以延伸到连续的量子过程中,为实施定量的模拟量子计算提出了一定的可能性.故而,错误缓解方法成为发挥近期量子计算机能力的必不可少的元素.
本文还对量子错误缓解的未来可能发展方向进行了讨论.我们认为量子错误缓解的发展具有巨大的潜力.由于实验上可以控制的量子比特数目,量子错误缓解将作为量子纠错的过度技术而存在,且为各类量子算法的实施提供保障.特别地,IBM等行业巨头在提供量子计算机云服务的同时,都考虑使用相应量子错误缓解技术作为实施算法的必要选项.注意到,机器学习算法在与量子纠错方法的结合中经历了相对较长时间、多种形式的发展,包括受限玻尔兹曼机、卷积神经网络和强化学习等[40-42].而目前,量子错误缓解技术在此领域仍存在大量未探索方向.——论文作者:张宇鹍1,2 袁骁3

 >
>