资源约束下城市轨道交通基础设施维修任务安排优化模型

发布时间：2021-08-04

　　摘要：针对城市轨道交通基础设施系统组成复杂、维修任务繁多、维修资源有限的特点，在分析不同类型维修任务需求的基础上，研究资源约束下基础设施维修任务的长期安排方法。考虑作业工队、维修设备等限制条件，建立基于混合整数规划的优化模型以安排任务的开始时间和持续时间，实现任务执行费用和惩罚费用的最小化。通过引入作业时间占用约束以减少任务作业冲突并提高维修任务安排的可实施性。针对约束复杂的大规模问题，设计综合求解器和启发式方法的并行混合算法进行求解。案例研究表明：考虑维修任务作业时间对提高维修任务安排的可实施性具有重要作用，所构建模型可有效协同安排不同类型的维修任务并节省维修费用，为城市轨道交通基础设施的长期维修任务安排提供决策支持。

　　关键词：铁路运输;维修任务安排;混合整数规划;基础设施;维修资源

　　0引言

　　城市轨道交通基础设施包括线路、供电、信号等若干系统，是列车安全和高效运行的关键。合理的长期维修任务安排对基础设施的质量均衡、降低维修成本和保障正常运行具有重要作用，并对短期任务安排和维修资源分配具有指导意义。

　　面向长期维修任务安排的方法通常需要考虑维修任务的作业需求和相关限制。根据维修任务特点，主要对周期性任务[1]、非周期性任务[2]、混合类型任务[3]进行优化编制，且关注维修任务的组织集中化和维修资源的分配均衡化。但以铁路系统基础设施为研究对象的优化方法较少考虑任务的作业冲突，难以直接应用于城市轨道交通基础设施系统。

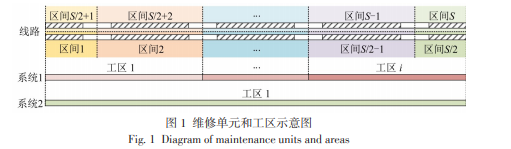
　　城市轨道交通系统要求在固定且有限的维修天窗内安排基础设施的维修任务，并避免对运营的不良影响[4]。天窗时间限制易导致维修任务安排冲突，需要调整任务作业时间[5]或分解维修任务[6]以减少任务的作业冲突，故增大了维修任务安排的复杂性。针对上述问题，本文考虑城市轨道交通基础设施各类维修任务的作业要求，引入维修工队、天窗时间等维修资源约束，研究城市轨道交通基础设施长期维修任务安排的优化方法。1问题描述城市轨道交通基础设施包含N个系统，各系统均设置若干个维修工区。工区由一定数量的相邻区间组成，区间是执行维修任务的最小单元。如图1所示，全线共分为S个区间，系统1在全线设有多个工区，而系统2只设一个工区。长期维修任务安排的时间被划分为等间隔的维修时段，考虑到一般维修任务的周期均以周或月为单位，因此年度维修任务安排以周为单位划分得到维修时段，设P为时段集合，|P|为时段数量。

　　根据维修任务的作业量、作业周期等差异，将任务分为日常维修和专项维修[3]。其中，日常维修任务可在一个时段内完成，且存在作业周期限制，所以同一区段上的日常维修任务在安排时段内需要重复执行。日常维修任务间存在包含关系，定义包含任务a的集合为Ga(a∈Ga)，其中的任务不能同时执行。专项维修任务的作业量较大，需在多个连续区间和时段内作业。专项维修任务包括执行周期超过任务安排时段的任务和大型维修任务，不会重复执行。

　　为优化安排时段内的总维修费用，需在满足维修任务需求的前提下，合理安排两类维修任务。为便于构建模型，提出如下假设：

　　(1)已知全部日常和专项维修任务的信息，不考虑安排时段中新增任务的情况。

　　(2)专项维修任务在连续多个时段中执行时，各时段内的作业量相同。

　　(3)专项维修任务需要专用的工队和维修设备，不与日常维修任务共享维修资源。

　　4案例研究

　　4.1案例背景

　　以某地铁线路为研究对象，线路共分为52个区间，基础设施中线路、供电、信号、机电系统设置5个维修工区，建安系统设置1个维修工区。年度维修任务安排在52个时段中，时段内可作业天数Qsp为7d，每天可作业时间Tsp为5h，时间占用比例限制Fsp为0.9，天窗时间占用冲突的惩罚费用cO,sp为1000元。

　　日常维修任务共有29项，基本参数如表2所示。包含其他任务和需要多个工队的任务费用分别为基础费用的2.5倍和4.0倍，组合维修的折减费用为任务执行费用的4%。专项维修任务共有200项，基本情况如表3所示，同时作业和非同时作业的任务各有50对。任务限制作业数量zR,p和zM,sp取值分别为6和3项，占用比例扩展系数ga为0.1。任务的执行费用和各项惩罚费用如表4所示。

　　4.2优化结果

　　并行混合求解算法的求解过程如图3所示。初始解(第1代)中2个子模型均应用时间占用比例限制的上限，所以存在较高的天窗时间占用冲突，为49.99。在1~3代中，占用冲突快速下降，但逐渐严格的占用约束增大了维修任务的费用(C1和C2)。第4~6代中，总时间占用冲突略有增加，但维修任务费用减少，使总费用下降。总费用逐渐趋于稳定并在第6代时实现收敛。

　　求解结果如表5所示，维修安排结果的总费用为263168.0元，其中85.89%来自维修任务，14.11%为惩罚费用，时间占用冲突占惩罚费用的51.32%。维修安排结果共包括200项专项维修任务和7902项日常维修任务，其中6625项任务实现与相同任务组合。

　　相关论文还可以参考：轨道交通运营管理论文怎么查找文献

　　为验证并行混合求解算法效果，使用求解器(Gurobi)对综合优化模型进行求解，结果如表6所示。线性化后的综合优化模型共包括1976048个决策变量和3390464个约束条件，求解器只能得到模型的理论下界。并行混合求解算法可在2.1h内得到可行解，与下界的差异为2.44%，说明并行混合求解算法具有较好的求解效率和精度。

　　4.3天窗时间占用约束的影响分析

　　3种不同天窗时间占用约束下的求解结果如表7所示，存在冲突的时空分布如图4所示。由于维修任务的集中安排可减少费用，在不考虑占用约束时(情形B)，维修任务安排结果中存在大量且显著的冲突，平均值为0.326。独立考虑两类维修任务的占用约束时(情形C)，占用冲突明显下降但冲突的数量降低不明显。情形A中，联合约束使得冲突数量和比例均有明显下降，平均占用冲突可降至0.089，维修任务的可实施性较高。占用冲突的减少会增加任务的执行费用和惩罚费用，日常维修任务费用的变化较小，因为灵活的任务间隔可避免任务安排在存在占用冲突的时段和区段内。上述结果说明，考虑任务的占用约束可有效降低冲突发生的数量和规模，降低进一步调整维修安排的复杂性。

　　4.4灵敏度分析

　　作为重要的维修资源，天窗时间将直接影响任务的可执行性。如图5所示，随着天窗时间的减小，总费用C逐渐增大，天窗时间每减少20min，总费用增大约4.0%。当天窗时间减少为240min时，模型无法得到可行解，需要增加工队数量以同时执行更多的任务。天窗时间对专项维修任务费用C2的影响较大，因为专项维修任务的作业量较大，需要更多的作业时段以减少在每个时段的时间占用。

　　维修任务的时间占用冲突与冲突的惩罚费用直接相关，如图6所示。随着惩罚费用的增加，占用冲突显著减小，惩罚费用增至5000元时占用冲突可降至7.81，说明维修任务安排结果的时间占用冲突存在较大的优化空间。同时，为降低天窗时间占用冲突，任务的执行费用会增加，导致总费用快速增加，因此需要平衡占用冲突和任务执行费用，实现合理的维修任务安排。

　　5结论

　　本文得到的主要结论如下：

　　(1)提出的维修任务安排优化模型可在满足任务执行需求的基础上有效降低维修费用，相比不考虑任务作业时间的方法能够降低81.74%的天窗时间占用冲突，提高维修任务的可执行性。

　　(2)天窗时间长度对维修任务安排有显著影响，缩短天窗时间需要增加维修工队数量以保证维修任务需求。天窗时间的占用冲突会随着惩罚费用的增加而显著减小，但需要平衡冲突规模与维修任务费用之间的关系。——论文作者：刘葛辉，陈绍宽*，刘爽，金华，王丹阳