多任务深度学习技术在储层横波速度预测中的应用

发布时间：2021-03-04

　　摘要储层参数与横波速度存在强非线性关系，难以用解析方程表达。深度学习具有强大的非线性寻解能力，可借助其优势构建横波速度与储层参数的映射关系，实现横波速度预测。前人研究主要采用单任务深度学习方法，输入多种储层参数曲线，只输出横波速度预测成果，这种方式存在一定的过拟合风险。为此，考虑到横波速度预测与其他测井评价任务的相关性与继承性，在横波预测模型训练之前首先开展岩性预测模型训练，利用权值共享的思想构建多任务学习模型，同时输出岩性预测成果和横波速度曲线。实践表明，相比多元拟合方法及单任务深度学习方法，该方法生成的岩石物理交会图在岩性分布上更为合理，不同岩性的横波速度预测精度都得到提升，其中含气砂岩段速度预测相对误差降低2%以上，证实了该方法具有较好的实用价值。

　　关键词深度学习;横波速度预测;多任务学习;迁移学习

　　0引言

　　实际生产中考虑测井的经济性，测井曲线中常遇到横波曲线缺失的现象。然而横波速度是进行岩石物理分析、叠前储层预测及储层AVO特征研究的必备信息，需要技术人员对缺失的横波速度进行重构(本文简称为横波预测)。横波预测主要有三大类方法，经验公式法、多元拟合法及岩石物理建模法。Gardner(1974)提出了饱含水岩石声波-密度关系式(Gardneretal.,1974)、Greenberg和Castagna(1992)提出了纵-横波经验关系式(Greenbergetal.,1992)，但由于储层参数与横波速度之间的强非线性关系，经验公式会产生较大误差。早期多元拟合技术主要通过建立目标曲线与其他测井曲线的线性关系完成预测，存在方程表达能力不足的问题，后来某些商业软件采用多种线性、非线性变换的拟合方法，增强了多元拟合方程的解析能力(李文成等,2014)，但该方法针对不同层段需人工选择参数组合方式，效率较低。岩石物理模型主要包括有效介质模型、自适应和散射理论模型、接触理论模型等(印兴耀等,2016)，Xu-White方法(Xuetal.,1996)是目前岩石物理建模的主要途径，众多学者对该方法的误差影响因素进行过讨论(孙璞等,2014;白俊雨等，2012;张元中等，2012)，但岩石物理模型的建立对研究人员的技术水平要求很高，且很难保证效率。另有一些学者研究了特定的横波重构技术，如基于最小平方法(王维红等,2019)、P-L模型法(罗水亮等,2016)、粒子群法(刘财等,2017)、误差校正法(黄为清等,2011)等，但普遍存在的问题是适用场景不足，部分方法原理复杂，实际应用过程繁琐。

　　在油气地球物理勘探领域，利用有限的观测数据(地震、测井、重磁数据)等进行储层预测及油气识别，本身就是一种建立复杂非线性映射关系的过程。而机器学习中的一些集成学习和深度学习的方法对复杂非线性求解具有优势。2016年以来，深度学习技术在地球物理领域的应用成果涌现，从层位自动追踪(Shietal.,2020)、相对地质年代追踪(Gengetal.,2020)、断层识别(Wuetal.,1996)、裂缝预测(丁燕等,2020)到地震岩相预测(刘力辉等,2019)中均有学者发表相应文章，实践表明深度学习技术可大大提升工作效率与预测精度。近两年来，有学者提出基于数据驱动的横波预测技术，比如利用基于集成学习思想的极端梯度提升算法的横波预测技术(闫星宇等,2019)，利用基于深度学习的全连接层神经网络(Salehietal.,2016)的横波预测技术，以及采用考虑了时间序列临近样本点相关性的LSTM及其变种GRU算法(王俊等,2020;孙宇航等，2020)的横波预测技术，均取得了不错的应用效果。

　　但上述研究方法都是基于单任务深度学习的方法，即单一的完成一种目标曲线预测。如果需要预测的曲线类型较多，将会导致多种任务的重复训练，并存在模型泛化能力不足等问题。然而在进行测井解释(如岩性、孔隙度、饱和度解释)、曲线重构(横波预测)的时候，多个任务之间是具有相关性的，可以采用迁移学习的方法，利用权值共享的思想将某个任务作为相关任务的初始权重。理论上讲，由于参与训练的样本标签变多，模型的泛化能力会更强，已经有学者将这种思想应用到断层解释及图像去噪中并取得良好效果(Wuetal.,2019)。此次研究通过构建多任务网络模型，将岩性预测训练模型作为横波预测的前置模型进行迁移学习，然后进行全局权重参数微调改善预测效果，同时输出岩性及横波预测成果，以达到提升预测成果的岩石物理交汇合理性，降低不同岩性段横波预测误差的目的。

　　1技术方法

　　1.1多任务深度学习

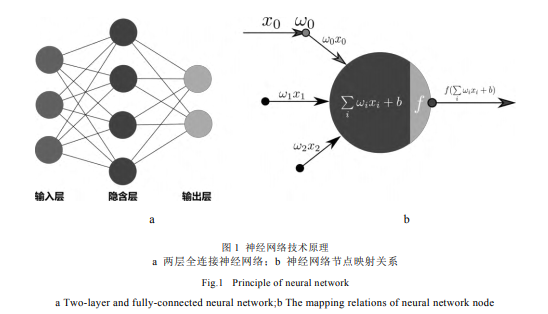
　　图1a为典型的两层全连接神经网络，包含一个输入层，一个隐含层和一个输出层，隐含层由四个节点组成。图1b为某节点的神经网络映射关系，隐含层接收输入层数据，针对数据每个维度ix，分配权重iw加权求和，并与偏置b求和，最后引入非线性函数f作为激活函数进行输出。通过以上操作，神经网络即可完成复杂的非线性映射任务。

　　为提升工作效率，防止由于任务目标的轻微改变而重复训练模型的问题，在实际生产中通常采用迁移学习的方法，将训练好的成熟模型应用到其他类似的目标任务中。具体来讲，即采用迁移学习中神经网络权值共享的思想，将成熟模型作为类似任务的初始权重，通过增加网络层数重新训练新任务。通过定义多个损失函数及输出项，网络结构可同时开展多任务学习，整个网络结构的损失函数由多个任务综合决定。在利用梯度下降等优化算法降低损失函数数值的时候，权重的更新会综合考虑多个任务与对应样本标签的匹配程度，形成全局最优的网络结构，见图2。

　　相关知识推荐：论文发表前怎么做更容易成功

　　通常在进行深度学习训练时，数据预处理、激活函数及损失函数的选取、隐含层及节点数的确定等是比较关键的步骤，而本次多任务深度学习涉及到两个不同的训练目标，在设计激活函数与损失函数的时候需要特别处理，实现步骤通过以下小节逐一进行介绍。

　　1.3激活函数和损失函数

　　岩性预测输出层采用sigmoid激活函数，横波预测输出层及其余层均采用ELU非饱和激活函数，这样可有效防止出现梯度消失的问题。在整个训练过程中，需要确定岩性分类及横波预测两个任务的损失函数，以及整个多任务学习网络结构总的损失函数。岩性分类预测模型的损失函数采用式(3)的交叉熵进行计算，其中N为总样本数，i为某一样本点，M为分类数量，j为某一分类(1：煤层，2：泥岩，3：砂岩，4：气砂)，ijy为指示变量(当该类别和样本i的类别相同就是1，否则是0)，ijp表示对于样本i属于类别j的预测概率;横波预测模型的损失函数采用均方差进行计算(4)，其中il表示第i个样本的观测值，~il表示第i个样本的预测值;多任务模型的损失函数由上述两个损失函数综合决定，其中W权重系数，取值范围为[0~1]。

　　1.4优化算法和更新策略

　　超参数空间寻优是深度学习的一大痛点，多任务深度学习面临同样的问题，本文对优化算法、学习率、迭代次数进行综合考虑。优化算法主要包括随机梯度下降法(SGD)、动量更新法(Momentum)、AdaGrad、RMSProp及适应性动量估计法(Adam)等，随机梯度下降法收敛速度快，但存在初始学习率选取困难、容易陷入局部次优解等问题，Adam(Kingmaetal.,2014)综合了AdaGrad及RMSProp方法的优点，梯度计算稳定性好，又可自然地实现步长退火，避免了学习率超参数的选择，本文采用该优化算法。同时，采用早停法更新策略(Keras,2020)，当验证集预测精度不在上升时停止迭代，避免了迭代次数的人为设定，早停法示意图见图4。

　　1.5隐含层数和节点数

　　由于涉及到多个损失函数，建立的多目标组合网络结构相比单任务复杂度提升，隐含层数与每层的节点数的变化对预测结果的影响程度变强，针对这两项超参数，本文采用超参数空间搜索寻优的方式确定。寻优方法主要有网格搜索法和随机搜索法，前者通过设定参数的分布区间，采用固定步长逐一进行训练，后者在超参数空间内随机选取参数进行训练(Bergstraetal.,2012)。两种搜索方式示意图见图5，浅灰色部分代表超参数空间，网格搜索的步长是固定的，因此可能会错过最优解，而随机搜索由于其在超参数空间位置的随机性，更可能获得最优解，本文采用了随机搜索的方式。

　　综上，本次多任务深度学习横波预测的完整实现方法见图6，文字表述如下：

　　1)如图6a，建立岩性预测网络结构，对输入数据进行标准化预处理，利用随机搜索确定超参数，开展模型训练并最终获得岩性解释模型;

　　2)如图6b，复用岩性训练模型的权值，开展迁移学习。对权值进行冻结处理(虚线框内)，将其输出与原始输入数据进行整合，统一作为横波预测模型的输入，利用随机搜索确定超参数并进行模型训练，最终获得横波预测模型;

　　3)如图6c，解冻岩性训练模型的权值，采用小步长(较大的步长会破坏已经形成的次优模型权值)对第二步获得的预测模型进行全局优化，获得岩性及横波预测多任务学习模型。

　　4)利用获得的多任务学习模型开展横波预测，获得预测结果。这种实现方法可有效的将岩性预测与横波预测关联起来，并通过引入岩性训练样本有效提升预测模型的泛化能力。

　　2实际应用

　　选取东海某凹陷斜坡带为靶区，该靶区为典型的砂泥岩地层，上部层系发育大套厚储层，含气特征不明显;下部层系发育薄砂层及煤层，煤系烃源岩为本区主要烃源岩，含气响应活跃。该靶区钻井较少，选取4口探井进行研究，由于横波速度通常受到岩性、物性的影响，选取伽马、纵波速度及密度三条曲线作为输入数据，三者与横波速度的关系如图7所示。

　　取四口井中的三口进行模型训练(共49087个样本点)，另一口井作为盲井(共14893个样本点)，检验预测效果。本文采用三种策略开展横波预测并对比预测效果，分别是某知名软件提供的多元拟合方法、基于全连接神经网络的单任务深度学习法及多任务深度学习方法。对单任务及多任务深度学习均采用了随机搜索方法确定隐含层及每个隐含层的节点数，限于篇幅仅展示多任务的随机搜索情况，见图8。从图中可以看出，随着隐含层节点的个数增加，预测精度开始提升，随着隐含层个数的增加，预测精度提升效果不明显，最优的参数组合如箭头指示。——论文作者：孙永壮1，黄鋆1