建立在相对安全率准则基础上的岩土工程可靠度分析与安全判据
时间:
摘要:各国规范普遍规定采用一次二阶矩法标定结构可靠度分析的安全指标。欧洲规范称其为“Level II”。为验证针对一个特定算例在目标可靠指标基础上标定的安全指标的普遍适用意义,提出“相对安全率”这一判据。简要回顾了使用一次二阶矩法计算相应目标可靠指标的允许安全系数和分项系数的原理和方法,然后改变被考核的算例的几何特征和岩土力学参数,要求“相对安全率”h R ,h F ,h P 互相接近(h 为相对安全率,下标 R,F,P 分别定义可靠指标、安全系数、分项系数 3 个领域的相应参数)。根据 Level II 标定的安全指标如能通过此普适性检验,则在工程实践中可以得到较广泛的认可。同时,回顾了这一方法在土石坝、加筋边坡、挡土墙、混凝土重力坝和拱坝的抗滑稳定分析中成功应用的研究成果,并对标定的结果做了总结。
关键词:岩土工程;可靠度分析;可靠指标;安全系数;分项系数;相对安全率
1 引 言
当今,全球化进程不断加速,基础设施建设规模不断增大,人们对工程结构安全的关注度日益增强,急需强化在规划设计工作中的安全保证体系[1]。基于可靠性分析基础上的设计方法(reliability based design,RBD,ISO2394)起源于欧洲、北美,并在日本、中国和发展中国家迅速推广。工程结构的可靠度分析为这一工作提供了理论基础,在此基础上建立起来的分项系数极限状态设计方法则为工程师提供了实际操作手段[2-8]。
岩土工程作为工程结构学科的一个分枝,相应的可靠度分析领域始终与土木工程学科同步推进[9-11]。但是,岩土力学有其独有的理论体系和框架,在纳入可靠度分析理论体系和推进分项系数极限状态设计方法方面也有特殊的问题需要处理。
(1) 关于安全系数和可靠度分析方法
在长期的实践中,岩土工程中的包括边坡稳定、地基承载力和土压力的各领域已形成行业内广泛被接受的安全系数体系。1995 年,美国国家科学研究委员会(National Research Council,1995)“岩土工程减灾可靠度方法研究委员会”提出了“岩土工程中的可靠度方法”的研究报告[6],这个报告的结论的第一段内容如下:“对于可靠度方法在岩土工程中作用的问题,委员会的主要发现是:可靠度方法,如果不是把它作为现有传统方法的替代物的话,确实可以为分析岩土工程中包含的不确定性提供系统的、定量的途径。在工程设计和决策中,用这一方法来定量地驾驭和分析这些不确实因素尤为有效。”
过去的 20 余年的实践过程表明,在岩土工程设计中用可靠度方法的判据代替安全系数的过程十分缓慢。大部分规范未能按结构可靠性设计规范的要求为设计人员提供可操作的分项系数,一小部分规范[12-13]提供了相关的判据,但据笔者所识,设计人员仍然把传统的安全系数复核成果作为他们评价建筑物安全的首先考虑的因素。
安全系数允许值在其形成的历史过程中并无太多的理论指导,是经验积累产物。现有的大坝、桥梁、高层建筑的规模早已远远超越了原有规范所覆盖的范围。例如,我国水利和水电行业为土石坝、混凝土重力坝和拱坝颁布的规范的总则中均明确注明仅适用于高度低于 200 m 的大坝[12-14]。但是,目前我国已建的坝高超过 200 m 大坝已趋常态化。于是,就要为超过 200 m 的大坝提供新的安全系数标准。在现阶段,面对出现的新情况提供新的安全系数允许值体系,单靠经验已难以实现。把结构可靠度分析理论作为建立岩土工程风险控制标准和准则的依据,提出在失效概率基础上的风险评估和分析方法,将成为科学、定量地研究和保证工程结构安全性的重要手段。本文节 4.1 介绍了笔者研究团队为土石坝的规范修订提供的新的判据即是一个有说服力的例子。
(2) 关于分项系数的标定工作
在岩土工程中,强度分项系数是一个将标准值转化为设计值的参数。ISO 2394 标准的定义是:“土性参数(如不排水抗剪强度)的标准值除以强度分项系数得到一个设计值,基于这一设计值的岩土工程承载力应大于设计荷载(荷载标准值乘以荷载系数) [3]”。
综观国内外关于分项系数的标定方法的论述,可以发现基本一致的建议是[1-4,9]:
① 结合本行业已积累的在安全系数方法基础上的大量工程实例,力求新的标准能反映已有的成功的实践经验。
② 在设定的目标可靠指标基础上通过一次二阶矩法找到强度指标设计值,为标定工作提供理论依据。
③ 综合考虑上述 2 个因素,为规范提供分项系数的建议值。
以上第 1 项工作自然是十分重要的。但是已有的工程经验往往是离散的、不完整的,在分析整理这些资料时,难免掺有主观成份,结果也难以有唯一性、权威性。为弥补这一缺陷,建立在可靠性理论基础上的第 2 项工作也是必不可少的。但是,令人遗憾的是,在现有规范的修编中,此类工作极少有见。
(3) 关于安全判据标定工作的普适性验证
基于可靠性分析基础上的设计方法(RBD)是通过目标可靠指标 b 确定强度指标的设计值,进而标定分项系数。一次二阶矩法(FOSM)即是开展这项工作的一个常用的手段。应用这一方法时,需要进行以下 2 个步骤的分析工作[15]:
① 对于一个典型工况,对设定的目标可靠指标求解相应的分项系数的初步标定值。
② 改变这一典型工况的体型和输入的随机变量的参数,确认上述初步标定值具有普遍适用意义。
如果只进行上述第 1 项工作而不开展与第 2 项内容相关的研究,那么,分项系数的理论标定工作仍然是不完整的、缺乏生命力的。
近年,笔者致力于为可靠度分析中的安全判据标定值的普适性验证提出了一个量化的判据,这就是相对安全率的判别准则。提出“相对安全率”方法以来,作者研究团队在混凝土重力坝和拱坝、高土石坝、重力式挡土墙和加筋土挡墙等领域开展抗滑稳定安全系数和分项系数的标定工作[15-22]。本文将系统回顾和总结这一工作,同时介绍在岩土工程抗滑稳定分析方面取得的最新研究成果。
2 岩土工程的安全判据以及定量联系
2.1 年计失效概率
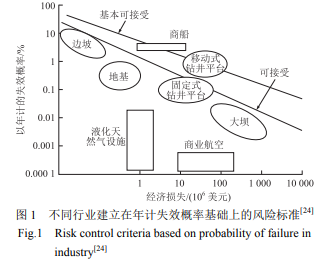
传统的风险分析和管理源于金融领域和保险业,并逐步在工业技术方面,同时形成了以年计失效概率作为风险控制标准的被广泛接受的准则[11,23]。图 1 对各行业对这一领域的相关内容作了较全面的回顾[24]。
结构风险分析通常首先研究在其生命周期的失效概率,下一个问题是如何将其转换成以年计失效概率。我们知道,规范在规定建筑物的允许可靠指标同时,规定了设计基准期。在水利水电工程中,一般将一级建筑物的设计基准年定为 100 a,其他建筑物则为 50 a。这样,允许可靠指标也可以与以年计的允许风险建立关系。
2.2 可靠指标
(1) 可靠指标与失效概率
确定了工程安全的允许风险标准,下一个问题则是如何计算某个工程的失效概率,以确认相关的设计是否满足了这一标准。 N. R. Morgenstern[25]将工程结构分析中包含的不确定因素分为三类,即管理因素、模型因素和参数因素。如果以 P(A),P(M)和 P(P)分别代表由上述管理因素、模型因素和参数因素导致的失效概率。
(3) 随机变量的特征参数和特征值
需要指出的是,上述工作是建立在随机变量的变异特性已知的前提下的。岩土材料的变异特性是岩土工程可靠度分析的另一专门的十分复杂的领域,有条件在已有大量相关的研究成果基础上总结可为本行业基本接受的建议值。本文在附录 A 的节 A2 中做了简要回顾。根据这些资料,在开展本文有关土方工程的可靠度分析时,对填筑土的黏聚力和摩擦系数的变异系数 Vc和 Vf 分别取 0.2 和 0.1。在完成所设定的为安全判据理论标定值后,也可在一定范围内变动输入的材料变异系数,进行敏感性分析,以提出最终的安全系数或分项系数的标定值,供规范编制工作参考。
在结构可靠度设计时,随机变量的均值自然是描述其特性的基本参数。但是,长期以来,很少有直接使用均值来进行设计计算的。在可靠度设计规范中对标准值的定义有不同层面和角度的解释。但是,在具体取值时,无非是要求使用一个相应一定保证率的分位数来确定材料强度指标的设计值[5,30-33]。例如,在土石坝的稳定分析时,中国规范一直要求使用材料试验强度的小值平均,也就是 0.25 分位值。美国陆军工程师团对土石坝设计强度指标的规定为 2/3 以上的试验数据大于采用值[11]。在岩土工程规范中,较多的情况是规定 0.2 分位数作为设计标准值。
2.3 安全系数的可靠度理论基础
(1) 建立在安全系数基础上的可靠指标表达式长期以来,在传统的岩土工程边坡稳定、土压力和地基承载力等领域已经形成了建立在安全系数基础上的安全评价体系和相应的计算方法。这些公式通常是非线性的,在引入可靠度设计方法时,不宜将这些计算公式强行改造成式(5)这样的表达形式。一个可行的途径是在原有的安全系数基础上的建立极限状态方程[34-38]。
3.5 小结:建立在相对安全率判据基础上的安全标准理论标定方法
本文的目的是在设定的目标可靠指标 ba 的条件下,为安全系数的允许值 Fa 和分项系数 c g 和 f g提供“理论标定值”。这一工作首先是针对一个目标可靠指标恰好为 ba 的特定案例进行的。依据节 2.3 和 2.4 阐述的方法,可为 Fa 和 c g 和 f g 提供“初步标定值”(见节 2.3 和 2.4 的算例)。本文提出的相对安全率判据旨在考察相应的“初步标定值”是否具有唯一性、可重复性。证明这一特性的数学命题是对同类问题,不管其几何参数和强度指标如何变化,始终能保证式(39)和(40)成立(见节 3.3 的算例)。满足此数学命题,则“初步标定值”即为根据 Level II 获得的“理论标定值”。
开展上述工作的前提是:
(1) 以岩土工程中已经建立起来的安全系数 F 为目标函数,按式(18)或(44)计算可靠指标。
(2) 安全系数 F 呈正态分布时,分别按式(31), (36)和(37)计算h F ,h R 和h P 。安全系数 F 呈对数正态分布时,按式(45)和(37)计算h F ,h R 和h P 。
(3) 在计算可靠指标时,假定随机变量的变异系数已知。对输入随机变量的变异系数的合理性的论证属另一独立的命题。但是,可以通过变异系数的敏感性分析为“理论标定值”可能的变动范围做出估计,以最终确定规范的建议值。在进行敏感性分析时,如果要求式(39)和(40)同时满足,变异系数的敏感性可以控制在一个较小的范围内。
以下讨论建立在“相对安全率”的安全判据理论标定方法在解决边坡、挡土结构和重力坝领域安全标准问题中的应用。
4 边坡稳定安全判据
4.1 堆石坝边坡安全系数标准研究
(1) 问题的提出
近 30 余年,有关堆石坝边坡安全系数标准的研究经历过 2 个阶段。第一阶段:堆石体坝坡采用非线性强度指标稳定安全系数标准的研究[33]。从 20 世纪 80 年代开始,混凝土面板堆石坝在我国大范围推广应用。在进行相关的坝坡稳定分析时发现,堆石材料的抗剪强度指标具有明显的非线性特性[43],对于高坝,这一特性更是不容忽视。
相关知识推荐:岩土工程评高级职称需要什么成果
在进行非线性稳定分析时,规范关于不同级别的大坝的安全系数允许值标准是否也要作相应的调整,这个问题曾是规范修订中的重点研究内容[14]。笔者研究团队使用可靠度分析原理对这一问题开展了相关的研究[33],最终的结论是,如果使用规范中规定的非线性强度指标的小值平均值,那么原有的规范规定同样适用。邓肯指数模式被水电土石坝设计规范采纳,进入了正式条文中。在该规范的“编制说明”中详细介绍了笔者的上述研究成果[14]。第二阶段:高度超过 200 m 的堆石体坝坡安全系数标准的研究[18-19]。我国已建及规划中的 200 m 以上的土石坝有:水布垭(233 m)、糯扎渡(261 m)、双江口(314 m)、两河口(295 m)、马吉(270 m)、如美(315 m)、茨哈峡(253 m)等。但是,现行碾压式土石坝设计规范[14]、混凝土面板堆石坝设计规范[44]均明文规定仅适用于坝高 200 m 以下大坝。为高度超过 200 m 的土石坝提供坝坡抗滑稳定最小安全系数的规定,是一个待解决的问题。在国家基础研究项目支持下,科研人员为特高坝提出了更高一个等级的风险标准,并提出将坝坡稳定允许安全系数提高到 1.6~1.7 的建议[19]。本节简要介绍上述应用可靠度分析方法解决工程实践中面临的基础理论问题的成果。 (2) 非线性强度坝坡稳定分析安全标准研究首先分析一个坝坡坡比为 1∶1.3,坝高 150 m 面板坝。在工程实践中,这是行业公认的具有典型意义的坝坡稳定问题,其筑坝材料为硬岩堆石料。相关研究表明,对于硬岩,压实堆石料的强度指标及其变异特性指标见表 2[33],确定性模型使用了强度指标的小值平均值。可靠度指标通过 Rosenbleuth 法计算确定,计算简图如图 10 所示。
计算结果见表 3,这一计算成果表明,如果对硬岩堆石料非线性强度指标采用具有代表意义的小值平均值,行业目前普遍采用的面板坝可接受的最陡坡度(1∶1.3)所相应的安全系数为 1.513,此值并不比规范对 1 级坝的要求 1.5 大很多。相应的可靠指标为 4.7 和允许值 4.2 相比,反映了稍高的抗滑稳定安全储备。这一研究结果说明,原有的土石坝规范关于各类等级的允许值的规定不需对非线性分析做额外的规定。
在笔者提出了相对安全率的判据后,将此例的坝高 75 m 变化至 200 m。获得的相关计算成果见表 4[19]。可见,相应不同坝高h R 和h F 十分接近,说明 Fa = 1.5 和 b a = 4.2 对于不同坝高均反映了相同的风险控制标准,Fa = 1.5 和 b a = 4.2 这一安全判据在非线性坝坡稳定分析中具有普适意义。——论文作者:陈祖煜

 >
>